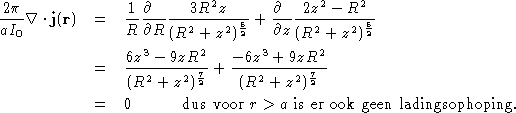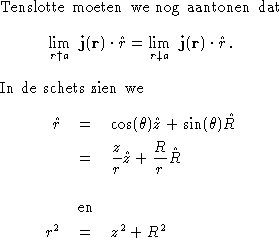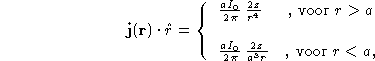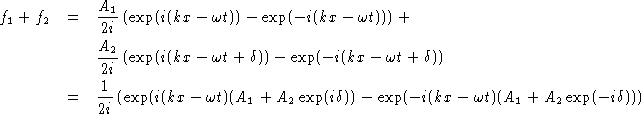-
De wet van ladingsbehoud in integrale vorm is:
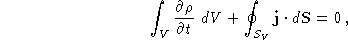
met 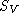 een gesloten oppervlak dat V omvat.
een gesloten oppervlak dat V omvat.
We werken nu de oppervlakte-integraal om naar een integraal over het
volume V met behulp van de stelling van Gauss:
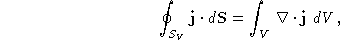
zodat
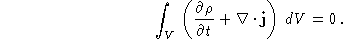
Omdat dit moet gelden voor een willekeurig volume V, moet de
integrand zelf nul zijn, zodat we uiteindelijk de wet van ladingsbehoud
in lokale vorm hebben verkregen:

-
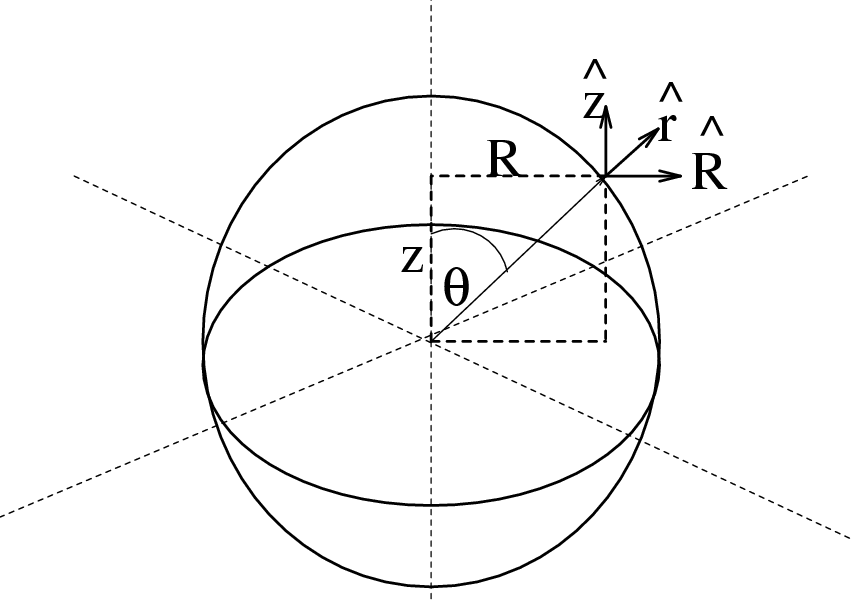
Gegeven is de (cilindersymmetrische) stroomdichtheidsverdeling binnen (r<a)
en buiten (r>a) een bol:
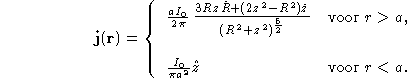
Er hoopt zich nergens lading op (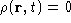 )
als geldt:
)
als geldt:

Eerst het geval r<a:

Nu voor r>a:
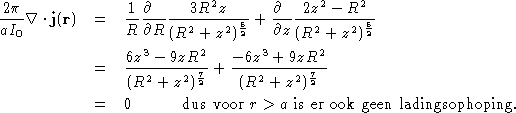
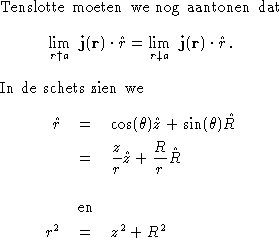
Gebruiken we dit, dan volgt na wat algebra:
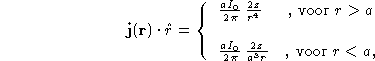
en hiervoor zijn onder- en bovenlimiet duidelijk gelijk.
-
a) triviaal.
b) triviaal.
-
a)
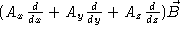
b) 0.
-
a)
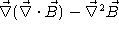 .
.
b) 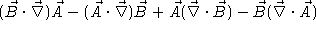 .
.
-
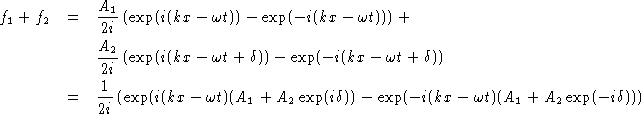
Definieer nu  zodanig dat
zodanig dat 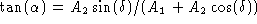 .
Verder is de lengte van
.
Verder is de lengte van 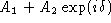 gegeven door
gegeven door 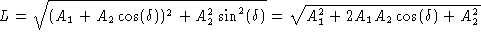 .
Dus het totaal levert
.
Dus het totaal levert
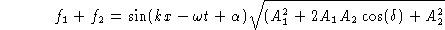
-
b) Door gebruik te maken van de Maxwell vergelijkingen in integrale vorm
kunnen we deze som oplossen. Voor de ladingsverdeling nemen een we schilletje
van straal R en dikte
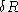 tussen deze platen. Verder nemen we een identiek schilletje buiten de twee
platen. Indien we de buitenranden met elkaar verbinden en ook de binnenranden,
kunnen we de eerste Maxwell vergelijking gebruiken; De ladingsdichtheid
per oppervlak wordt dan gegeven door:
tussen deze platen. Verder nemen we een identiek schilletje buiten de twee
platen. Indien we de buitenranden met elkaar verbinden en ook de binnenranden,
kunnen we de eerste Maxwell vergelijking gebruiken; De ladingsdichtheid
per oppervlak wordt dan gegeven door:

of voor de beide oppervlakken geldt
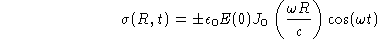
De stroomdichtheid wordt bepaald door een ``raampje'' te maken langs
de 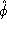 richting wederom door een van de oppervlakken; Maxwel IV geeft dan
richting wederom door een van de oppervlakken; Maxwel IV geeft dan
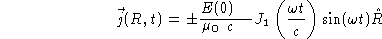
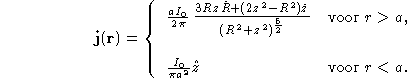
![]() )
als geldt:
)
als geldt: