
How many lowest modes in a solid of size L?
Density of lowest modes ~ (Number of lowest modes) / (frequency)(volume)
Trick to find lowest modes:
remove boundary constraints,
count free modes with 0 frequency
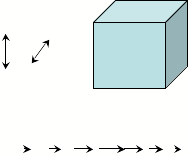
---3 translations.. eg
Re-apply boundary constraints: walls fixed
pure
translations are no longer possible
lowest modes
are distorted translations
Frequency w0(L) ~ 1/L
Density of lowest modes ~ (Number of lowest modes) /
(frequency)(volume)
3
1/L
L3
~ L-2
Since frequency ~ 1/L, density of lowest modes ~
frequency2
cf jammed solids: they must have
lots of lowest modes or
very small w0(L)
which?