![]() en
en ![]()
Met ![]() en q2v2=I2dy volgt de totale kracht als de integraal
over Fr(y),
en q2v2=I2dy volgt de totale kracht als de integraal
over Fr(y), ![]() . Hierbij merken we op dat er geen kracht
is parellel aan de stroomdraad, omdat de bijdrage van y wegvalt tegen die
van -y, Fy(-y)=-Fy(y). De integraal over een oneven functie is nul.
. Hierbij merken we op dat er geen kracht
is parellel aan de stroomdraad, omdat de bijdrage van y wegvalt tegen die
van -y, Fy(-y)=-Fy(y). De integraal over een oneven functie is nul.
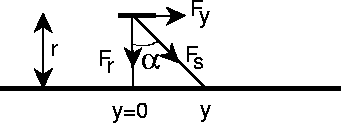
Uiteraard zijn er meerdere manieren om de integraal te bereken. De figuur
suggereert de substitutie ![]() . We vinden dan eenvoudig
. We vinden dan eenvoudig ![]() .
Als y tussen plus en min oneindig loopt, loopt
.
Als y tussen plus en min oneindig loopt, loopt ![]() tussen
tussen ![]() en
en ![]() . Samen met
. Samen met ![]() vinden we
dus
vinden we
dus ![]() . Voor I1=I2=I en
. Voor I1=I2=I en ![]() m vinden we dus
m vinden we dus ![]() .
.