- 7.
- a.
- Voor deze situatie werkt het Doppler-effect "dubbel". Ten eerste: de frequentie
die de auto terugkaatst is, in het ruststelsel van de auto, gelijk aan die
wordt opgevangen. De frequentie die de naderende auto opvangt is een
factor
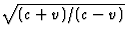 hoger dan die is uitgezonden, t.g.v. de Doppler
verschuiving. In het ruststelsel van de auto is de teruggekaatste straling
derhalve eveneens een factor
hoger dan die is uitgezonden, t.g.v. de Doppler
verschuiving. In het ruststelsel van de auto is de teruggekaatste straling
derhalve eveneens een factor 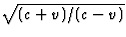 hoger. Ten tweede: voor
de waarnemer aan de kant van de weg wordt de echo van de auto uitgezonden door
een naderende bron, en heeft de echo dus een hogere frequentie dan in het
ruststelsel van de auto. Dit geeft wederom een factor
hoger. Ten tweede: voor
de waarnemer aan de kant van de weg wordt de echo van de auto uitgezonden door
een naderende bron, en heeft de echo dus een hogere frequentie dan in het
ruststelsel van de auto. Dit geeft wederom een factor 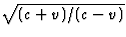 .De echo was dus hoger dan het uitgezonden signaal,
.De echo was dus hoger dan het uitgezonden signaal, 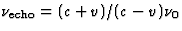 . Een goede benadering voor auto's is
. Een goede benadering voor auto's is 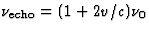 . Hieruit volgt
. Hieruit volgt 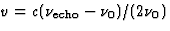 .
Gegeven is dat
.
Gegeven is dat 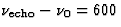 Hz, zodat v=37,5 m/s=135 km/u.
Hz, zodat v=37,5 m/s=135 km/u.
- b.
- Met bron en waarnemer omgedraaid (maar dat maakt bij het relativistische
Doppler-effect voor electro-magnetische straling niet uit, dit in tegenstelling
tot het Doppler-effect voor geluid !), is de analyse precies eender als bij
(a). Voor de planeetbewoner werkt het Doppler-effect alleen de eerste keer,
zodat
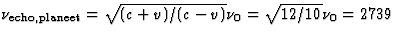 MHz. Voor het ruimteschip werkt het Doppler effect ook de tweede keer, zodat
MHz. Voor het ruimteschip werkt het Doppler effect ook de tweede keer, zodat
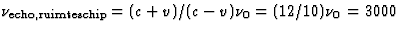 MHz. (De
benadering als bij (a) geldt hier uiteraard niet).
MHz. (De
benadering als bij (a) geldt hier uiteraard niet).
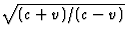 hoger dan die is uitgezonden, t.g.v. de Doppler
verschuiving. In het ruststelsel van de auto is de teruggekaatste straling
derhalve eveneens een factor
hoger dan die is uitgezonden, t.g.v. de Doppler
verschuiving. In het ruststelsel van de auto is de teruggekaatste straling
derhalve eveneens een factor 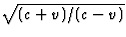 hoger. Ten tweede: voor
de waarnemer aan de kant van de weg wordt de echo van de auto uitgezonden door
een naderende bron, en heeft de echo dus een hogere frequentie dan in het
ruststelsel van de auto. Dit geeft wederom een factor
hoger. Ten tweede: voor
de waarnemer aan de kant van de weg wordt de echo van de auto uitgezonden door
een naderende bron, en heeft de echo dus een hogere frequentie dan in het
ruststelsel van de auto. Dit geeft wederom een factor 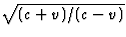 .De echo was dus hoger dan het uitgezonden signaal,
.De echo was dus hoger dan het uitgezonden signaal, 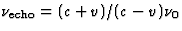 . Een goede benadering voor auto's is
. Een goede benadering voor auto's is 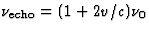 . Hieruit volgt
. Hieruit volgt 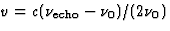 .
Gegeven is dat
.
Gegeven is dat 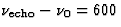 Hz, zodat v=37,5 m/s=135 km/u.
Hz, zodat v=37,5 m/s=135 km/u.
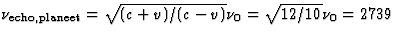 MHz. Voor het ruimteschip werkt het Doppler effect ook de tweede keer, zodat
MHz. Voor het ruimteschip werkt het Doppler effect ook de tweede keer, zodat
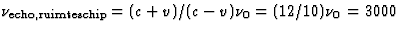 MHz. (De
benadering als bij (a) geldt hier uiteraard niet).
MHz. (De
benadering als bij (a) geldt hier uiteraard niet).