4. Lorentz transformaties

De traditionele interpretatie van het relativiteitsprincipe, zoals we dat hebben besproken is erg voor de hand liggend, maar niettemin toch onjuist. In de gebruikte transformatieformules is als vanzelfsprekend aangenomen dat de tijd in S en S' het zelfde is. De nieuwe coördinaten x', y' en z' zijn lineaire functies van de oude coördinaten x, y en z en de tijd t. Voor de nieuwe tijd t' hebben we gewoon t'=t genomen. Om hier de nadruk op te leggen hebben we dit in (3.3) voor de Galilei transformatie expliciet vermeld. Merk op dat dit een lineaire transformatie van vier variabelen naar vier nieuwe variabelen is.

Als we algemeen zouden zoeken naar een lineaire transformatie $(x,y,z,t)\rightarrow(x',y',z',t')$, met de eigenschap dat eenparige rechtlijnige bewegingen weer in eenparige rechtlijnige bewegingen overgaan, dan zou de conditie t'=t ervoor zorgen dat we op de Galilei transformaties zouden uitkomen. Als we de eis t'=t laten vallen en toelaten dat de nieuwe tijd t' niet alleen van de oude tijd t maar ook van de oude ruimte coördinaten x, y en z afhangt zijn er ook andere mogelijkheden. Het betekent dat we tijd en ruimte niet langer als afzonderlijke begrippen opvatten, maar dat we denken aan een 4-dimensionale ``ruimte-tijd''. Dit is de essentie van de gedachtengang van Einstein.

Het beroemde gedachtenexperiment van Einstein met de rijdende trein - die ook als voorbeeld dienst doet om aan te duiden dat eenparige beweging een relatief begrip is (en wie heeft niet die sensatie van verwarring gehad om te besluiten of de trein nu wel of niet rijdt als U alleen maar de trein naast U kan zien) - laat zien dat gelijktijdigheid, in de Newtonse theorie nog zo vanzelfsprekend, met een waarnemer-onafhankelijke lichtsnelheid plots geheel op zijn kop wordt gezet. Laat hiertoe een lichtflits vanuit het midden van de trein naar beide kanten zich uitspreiden. Voor een waarnemer in de trein bereikt het licht de voor- en achterkant van de trein precies gelijktijdig, maar voor een waarnemer op het perron wordt de achterkant eerder bereikt dan de voorkant, zoals U eenvoudig nagaat gebruikmakende van het feit dat ook voor de waarnemer op het perron het licht zich met de snelheid c voortbeweegt!

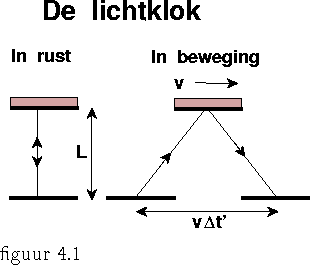
psfile=lichtklok.ps figuur 4.1

Evenzeer kunnen we de zg. tijdsdilatatie op uiterst eenvoudige wijze demonstreren. We gebruiken hierbij een zg. lichtklok die bestaat uit een ontvanger/zender met erboven, op een afstand L, een spiegel. De tijd verstreken tussen het zenden en ontvangen, na reflectie tegen de spiegel, van een foton kunnen we als één tijdseenheid beschouwen. Noem deze $\Delta t=2L/c$. Anderzijds, voor een bewegende waarnemer (loodrecht op de verbinding tussen spiegel en zender/ontvanger, die dus geen contractie ondervindt) geldt nog steeds dezelfde snelheid van het licht, maar beschrijft dit nu de weg van een driehoek met een basis $v\Delta t'$ en een hoogte L. De verstreken tijd $\Delta t'$ tussen het zenden en ontvangen van een foton, zoals waargenomen door de bewegende waarnemer is nu evenzo de totale afgelegde weg van het foton gedeeld door de lichtsnelheid, dus $c\Delta t' = 2\sqrt{L^2+(v\Delta t'/2)^2}$. Aangezien $L=c\Delta t/2$ vinden we nu eenvoudig de beroemde tijdsdilatatie
\Delta t'=\Delta t/\sqrt{1-v^2/c^2}. (4.1)

De tijdsdilatie is bevestigd in experimenten waar de cosmische straling wordt bestudeerd. Hoog in de atmosfeer, op een hoogte van ca. 10 km, komt cosmische straling (zeer hoog-energetische fotonen of snelle deeltjes) in botsing met de lucht en vinden er kernreakties (en verstrooiing) plaats. Dat is maar goed ook, want zeer harde straling is niet gezond voor mens en dier. Een van de deeltjes die bij zo'n reactie in grote hoeveelheden worden geproduceerd is het muon, dit is een zwaardere uitvoering van het electron met een massa van ca. 206,77 maal de massa van het electron. Het muon is zelf instabiel en valt in ca. $\tau=2,2\times 10^{-6} s$ weer uiteen in bijv. een electron en twee neutrino's. Op basis van de Newtonse mechanica zou, zelfs bij een snelheid van het muon die dicht tegen de lichtsnelheid zit, het muon slechts 660 meter afleggen voordat het vervalt (strikt gesproken verloopt het verval met een kansverdeling die beschreven wordt door een e-macht, $e^{-t/\tau}$). Na 10 km zijn dan praktisch alle muonen vervallen, maar dit is in tegenspraak met de waarnemingen. Vanuit het standpunt van de waarnemer verloopt het vervalsproces van een bewegend muon echter met een tijd $\tau'=\tau/\sqrt{1-v^2/c^2}$ en bij een snelheid v=0,998 c is de afgelegde afstand gelijk aan de te overbruggen afstand van 10 km. Hoe dichter de snelheid van het muon de snelheid van het licht nadert hoe meer muonen nog niet vervallen zijn voordat ze het aardoppervlak bereiken. Vanuit het oogpunt van het muon wordt de afstand tot het aardoppervlak verkort met een factor $\sqrt{1-v^2/c^2}$ en hoeft het dus bij een snelheid van 0,998 c, inplaats van de 10 km, maar 660 m te overbruggen. De conclusie is in beide gevallen dezelfde; door relativistische effecten kan het muon het aardoppervlak bereiken voordat het is vervallen. Ook in deeltjesversnellers, waar snelheden dicht bij die van het licht worden bereikt, leven onstabiele deeltjes aanzienlijk langer dan in rust. Men heeft dan ook plannen om cirkelvormige versnellers te bouwen waarin muonen versneld worden. Het grote voordeel is dat het energieverlies dat optreedt door de remstraling in een cirkelvormige baan evenredig is met E2/m4. Bij gelijke energie van het deeltje, verliest een electron maar liefst 1.6 miljard maal meer energie dan een muon. Uiteraard moeten de muonen gemaakt worden met zeer grote snelheid, want anders zijn ze vervallen voordat ze versneld kunnen worden. Men is nu op een punt gekomen waar zo'n muonversneller technisch haalbaar lijkt.

Nu het duidelijk is dat tijdsdilatatie ook werkelijk experimenteel is aangetoond moeten we ons afvragen of het voor ieder soort klok apart moet worden gecontroleerd. Dat zou uiteraard een ramp zijn en het doel van een fysicus is altijd wetten op te stellen die zo universeel mogelijk zijn, zodat ze ook een maximaal voorspellende waarde hebben. Die universaliteit van de de tijdsdilatatie is echter heel eenvoudig aan te tonen. Bijv. kunnen we i.p.v. de lichtklok een tennisklok maken, waarbij een tennisbal tegen de spiegel terugkaatst. Als we het zo inrichten dat de tennisbal terug is gekeerd, nadat het licht een geheel aantal keren, zeg n, heen en weer is gegaan (we kiezen n voldoende groot om te zorgen dat de tennisbal een realistische snelheid nodig heeft en we verwaarlozen uiteraard energieverliezen). Omdat een gebeurtenis op dezelfde tijd en dezelfde plaats (het samenvallen van de terugkeer van de tennisbal en het foton - na n reflecties) in ieder stelsel natuurlijk hetzelfde is (alleen gelijktijdigheid voor gebeurtenissen op verschillende plaatsen is niet langer gegarandeerd), zullen deze twee klokken in ieder stelsel gelijk lopen. Dit geldt uiteraard ook voor klokken die op een heel ander principe rusten, waarbij we via een wijzerplaat de klokken op dezelfde plaats met elkaar kunnen vergelijken. Dus de tijdsdilatatie is universeel en het is niet een eigenschap van de klok maar van de tijd die tot tijdsdilatatie aanleiding geeft.

Voordat we de Lorentz transformatie bespreken geven we nog een eenvoudige afleiding voor de regels van het optellen van snelheden. Dat ook hier iets bijzonders gebeurt is direkt duidelijk uit het lichtpostulaat.

Opgave 5:

Beredeneer waarom bij het optellen van een willekeurige snelheid bij de lichtsnelheid, we altijd weer de lichtsnelheid moeten krijgen.

Het toepassen van de Newtonse regels op dit feit zou leiden tot de vergelijking c=c+u, voor willekeurige u, en dit zou alleen kunnen als c oneindig is, in tegenspraak met de feiten. Om te zien hoe snelheden optellen, beschouwen we een zeer elegant gedachtenexperiment van N.D. Mermin. Hierbij wordt achter in een rijdende trein tegelijk een lichtflits en een kogel (met snelheid v) naar de voorkant geschoten. Het licht wordt gereflecteerd aan een spiegel op de voorwand en ontmoet de kogel op een fractie f van de totale lengte van de trein. De fractie f geeft een gebeurtenis die samenvalt in ruimte en tijd (de kogel ontmoet het terugkerende foton) en zal door waarnemers die t.o.v. de trein bewegen als dezelfde gemeten worden. Laat de trein met een snelheid u t.o.v. een waarnemer bewegen (de waarnemer beweegt dus met een snelheid -u t.o.v. de trein).

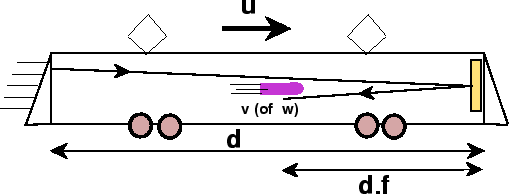
psfile=mermin.ps
figuur 4.2

We berekenen nu wat voor die waarnemer f is. De snelheid van de kogel in de trein, t.o.v. van de waarnemer buiten, noemen we w, en de lengte van de trein zoals door de waarnemer gemeten noemen we d (de waarde van d zelf is niet relevant, maar als U wilt kunt U 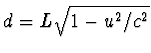$d=L\sqrt{1-u^2/c^2}$ nemen, met L de lengte van de trein in rust). We vinden nu w(T1+T2)=c(T1-T2), zijnde de netto afstand gemeten vanaf de achterkant tot het punt waar kogel en foton elkaar ontmoeten. Hieruit volgt T2/T1=(c-w)/(c+w). Anderzijds geldt ook dat cT1=d+uT1, zijnde de afstand die het foton tot het punt van reflectie aflegt. Evenzo is de afstand van de spiegel tot het ontmoetingspunt met de kogel gegeven door cT2=fd-uT2. Hieruit is d te elimineren en volgt T2/T1=f(c-u)/(c+u). Het gelijkstellen van deze twee uitdrukkingen voor T2/T1 leidt tot

f=f(u,w)=\frac{[c+u][c-w]}{[c-u][c+w]}.

Deze afleiding geldt voor iedere waarnemer, i.h.b. voor een waarnemer die met de trein meereist. Voor deze waarnemer moet u=0 en w=v worden genomen, en geldt f=f(0,v)=(c-v)/(c+v). Omdat f voor beide waarnemers hetzelfde moet zijn volgt dus de uitdrukking voor w, die leidt tot het ``optellen'' van de snelheden u en v:
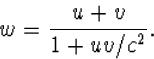w={u+v\over{1+uv/c^2}}. (4.2)

  • Volgende paragraaf
  • Naar inhoudsopave