Als we een aantal Lorentz transformaties met verschillende snelheden in
dezelfde richting achter elkaar uitvoeren is het totale resultaat weer een
Lorentz transformatie. We kunnen de snelheid als parameter voor zulke
transformaties gebruiken. Deze snelheden tellen echter niet op, zo als we
gezien hebben. Het is daarom soms handig om een andere parameter in te
voeren die wel additief is. We bekijken standaard Lorentz transformaties in
de x-richting zoals gegeven door formules (4.37) en definiëren een
door de snelheid u bepaalde parameter ![]() volgens
volgens
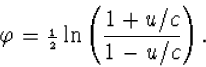
| (4.43) |
Beschouw nu de in bovenstaande opgave beschreven situatie: Drie
inertiaalsystemen S, S' en S'', met standaard Lorentz
transformaties ![]() en
en
![]() behorende bij snelheden u1 en
u2 in de x-richting. Geef de snelheid behorende bij
de resulterende transformatie
behorende bij snelheden u1 en
u2 in de x-richting. Geef de snelheid behorende bij
de resulterende transformatie
![]() aan als u. Deze u kan met formule
(4.42) in u1 en u2 uitgedrukt worden.
Volgens (4.43) hoort bij u1 de parameter
aan als u. Deze u kan met formule
(4.42) in u1 en u2 uitgedrukt worden.
Volgens (4.43) hoort bij u1 de parameter
![]()
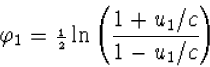 |
(4.44) |
en bij u2 de parameter
![]()
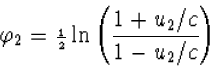 |
(4.45) |
Tenslotte hoort bij de snelheid u van de samengestelde transformatie de
parameter
![]() volgens
volgens
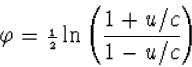 |
(4.46) |
Deze ![]() wordt met behulp van (4.42) uitgedrukt in u1
en u2:
wordt met behulp van (4.42) uitgedrukt in u1
en u2:
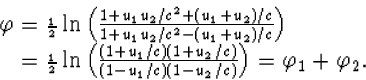 |
(4.47) |
We hebben dus gevonden dat de waarden van deze nieuwe parameter bij
opeenvolgende Lorentz transformaties in de zelfde richting optellen; de
parameter ![]() is additief. Uiteraard is alles wat we hier voor
Lorentz transformaties in de x-richting bespreken op de zelfde manier
van toepassing op transformaties in de y- en de z-richting.
is additief. Uiteraard is alles wat we hier voor
Lorentz transformaties in de x-richting bespreken op de zelfde manier
van toepassing op transformaties in de y- en de z-richting.
We gaan de Lorentz transformatie (4.37) in termen van
![]() schrijven. Uit de definitie (4.43) volgt
schrijven. Uit de definitie (4.43) volgt
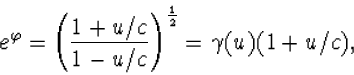 |
(4.48) |
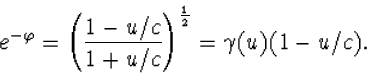 | (4.49) |
We herinneren ons de definities van de hyperbolische trigoniometrische functies
| (4.50) |
| (4.51) |
en daarmee
| (4.52) |
Deze hyperbolische sinus, cosinus en tangens hebben natuurlijk niets te
maken met hoeken of meetkunde; het zijn functies die wat hun eigenschappen
betreft wiskundige analogieën met de gewone trigoniometrische functies
vertonen. Met behulp van deze functies krijgen we uit (4.48) en (4.49)
| (4.53) |
| (4.54) |
en de bij (4.43) behorende inverse relatie
| (4.55) |
We schrijven hiermee tenslotte de Lorentz transformatie (4.37) als
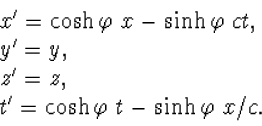 |
(4.56) |
De wiskundige analogie van de parameter
![]() met een hoek variabele zien we ook nog als we (4.56)
vergelijken met de formules voor een ruimtelijke draaiing van het assenstelsel
om de z-as over een hoek
met een hoek variabele zien we ook nog als we (4.56)
vergelijken met de formules voor een ruimtelijke draaiing van het assenstelsel
om de z-as over een hoek
![]()
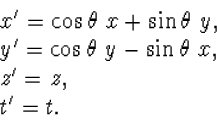 |
(4.57) |
Men noemt daarom de parameter
![]() soms wel pseudo-hoek.
soms wel pseudo-hoek.
Toepassing:
Bekijk inertiaalsystemen S0 , S1,
![]() Sn. Veronderstel dat iedere
Sk zich ten opzichte van Sk-1
met een snelheid u beweegt. We willen weten wat de snelheid
un van Sn ten opzichte van
S0 is. Voor Galilei transformaties zou dat gewoon n
maal u zijn, bij Lorentz transformaties is het een ingewikkelder
uitdrukking. We kunnen proberen u stapsgewijze te berekenen met formule
(4.42), maar het wordt snel duidelijk dat het niet zal meevallen op deze manier
een gesloten uitdrukking voor un te vinden.
Sn. Veronderstel dat iedere
Sk zich ten opzichte van Sk-1
met een snelheid u beweegt. We willen weten wat de snelheid
un van Sn ten opzichte van
S0 is. Voor Galilei transformaties zou dat gewoon n
maal u zijn, bij Lorentz transformaties is het een ingewikkelder
uitdrukking. We kunnen proberen u stapsgewijze te berekenen met formule
(4.42), maar het wordt snel duidelijk dat het niet zal meevallen op deze manier
een gesloten uitdrukking voor un te vinden.
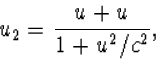 |
(4.58) |
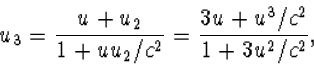 |
(4.59) |
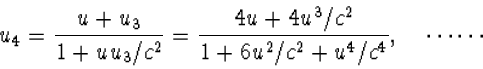 | (4.60) |
Met de pseudo-hoekvariabele is dat echter erg gemakkelijk. Volgens (4.55) geldt
| (4.61) |
De pseudo-hoekvariable is additief en dus is
![]() gelijk aan n maal
gelijk aan n maal
![]() . We kunnen daarom (4.61) met behulp van (4.48) en (4.49)
schrijven als
. We kunnen daarom (4.61) met behulp van (4.48) en (4.49)
schrijven als
![u_n=c\frac{[1+u/c]^n-[1-u/c]^n}{[1+u/c]^n+[1-u/c]^n}.](img133.gif) |
(4.62) |
We schrijven (4.62) nog een beetje anders
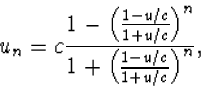 | (4.63) |
en zien dan dat de snelheid un bij toenemende n wel steeds groter wordt maar niet naar oneindig gaat, zoals dat bij Galilei transformaties zou gebeuren. In plaats daarvan nadert un van beneden naar de lichtsnelheid c als limietwaarde. Dit illustreert een belangrijk fysisch principe:
| Volgens de Einsteinse relativiteitstheorie kunnen deeltjes zich niet sneller bewegen dan het licht. De lichtsnelheid is een bovengrens. |
|---|
De conclusie dat niets zich sneller dan het licht kan voortbewegen lijkt in tegenspraak met wat in de astronomie bij quasars wordt waargenomen, waar gaswolken met grote snelheden worden uitgestoten. Er worden schijnbare snelheden gemeten die enkele malen groter dan de lichtsnelheid zijn.
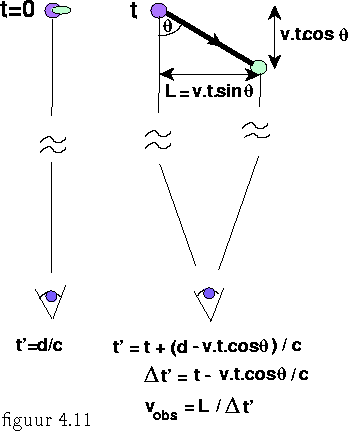
In de figuur is de situatie weergegeven. We stellen het tijdstip van de
explosie in de quasar op t=0. We zien deze explosie op aarde op het tijdstip
t'=d/c, waarin uiteraard d de afstand tot de
quasar is. Als de gaswolk zich onder een hoek
![]() (met de gezichtslijn van de quasar) beweegt, dan bereikt het
licht van de gaswolk de waarnemer verhoudingsgewijze eerder naarmate deze hoek
dichter bij nul ligt, eenvoudigweg omdat het licht een kleinere afstand af te
leggen heeft om de waarnemer te bereiken. Deze vermindering in afstand bedraagt
(met de gezichtslijn van de quasar) beweegt, dan bereikt het
licht van de gaswolk de waarnemer verhoudingsgewijze eerder naarmate deze hoek
dichter bij nul ligt, eenvoudigweg omdat het licht een kleinere afstand af te
leggen heeft om de waarnemer te bereiken. Deze vermindering in afstand bedraagt
![]() , waarin t de tijd is die verstreken is sinds de
explosie. De gaswolk wordt waargenomen op het tijdstip
, waarin t de tijd is die verstreken is sinds de
explosie. De gaswolk wordt waargenomen op het tijdstip
![]() . De waarnemer blijft de quasar uiteraard
opdezelfde plaats aan de hemel zien (aannemende dat de eigenbeweging
verwaarloosd kan worden). Voor de waarnemer is het verschil in tijd verstreken
tussen het waarnemen van de explosie en het waarnemen van de verwijderende
gaswolk
. De waarnemer blijft de quasar uiteraard
opdezelfde plaats aan de hemel zien (aannemende dat de eigenbeweging
verwaarloosd kan worden). Voor de waarnemer is het verschil in tijd verstreken
tussen het waarnemen van de explosie en het waarnemen van de verwijderende
gaswolk ![]() . De in die tijd door de gaswolk
afgelegde transversale afstand bedraagt
. De in die tijd door de gaswolk
afgelegde transversale afstand bedraagt
![]() , zodat het voor de waarnemer lijkt alsof de gaswolk de
volgende snelheid heeft:
, zodat het voor de waarnemer lijkt alsof de gaswolk de
volgende snelheid heeft:
| (4.64) |
Dit is dus een factor ![]() groter dan de
transversale snelheid
groter dan de
transversale snelheid ![]() . Deze transversale snelheid is
kleiner dan de werkelijke snelheid, en dus zeker kleiner dan de lichtsnelheid.
Nemen we als voorbeeld v=4c/5 en
. Deze transversale snelheid is
kleiner dan de werkelijke snelheid, en dus zeker kleiner dan de lichtsnelheid.
Nemen we als voorbeeld v=4c/5 en
![]() , dan kunt U eenvoudig na rekenen dat
vobs=4c/3, en dus beduidend groter dan de
lichtsnelheid.
, dan kunt U eenvoudig na rekenen dat
vobs=4c/3, en dus beduidend groter dan de
lichtsnelheid.
Uit dit voorbeeld zien we dat heel zorgvuldig geanalyseerd dient te worden wat we nu eigenlijk waarnemen, voordat we beweren dat er een tegenspraak is.
In de later ontwikkelde quantumtheorie is gebleken dat een lichtgolf zich onder bepaalde omstandigheden gedraagt als een deeltje. Een dergelijk deeltje wordt foton genoemd. Fotonen bewegen zich altijd met de lichtsnelheid c. In de elementaire-deeltjesfysica heeft men nog een ander type deeltje gevonden dat zich ook met de lichtsnelheid beweegt: het neutrino. Alle andere deeltje hebben snelheden die kleiner zijn dan c. We zullen later nog zien dat deeltjes die met de lichtsnelheid bewegen volgens de relativiteitstheorie massa nul hebben.