We hebben in hoofdstuk 4, vanaf formule (4.24) op pagina 17, een
parametrisering van de wereldlijn van een bewegend puntdeeltje gebruikt om
transformatieformules voor snelheden en versnellingen af te leiden. Deze
parametrisering ![]() was onafhankelijk van het gebruikte
inertiaalsysteem, maar verder nog willekeurig.
was onafhankelijk van het gebruikte
inertiaalsysteem, maar verder nog willekeurig.
We gaan gaan nu een heel bepaalde parametrisering van dit type invoeren, die om verschillende redenen erg handig is, en die bovendien een duidelijke fysische betekenis heeft. Beschouw de wereldlijn van een deeltje, zoals voor het 2-dimensionale geval getekend is in figuur 6.8. De snelheid van het deeltje hoeft niet constant te zijn. We benaderen de beweging door een opeenvolging van kortdurende eenparig rechtlijnige bewegingen. Voor het i-de tijdsinterval (ti,ti+1 ) geldt dat de constante snelheid vi gelijk is aan
| vi=(xi+1-xi)/(ti+1-ti). | (6.10) |
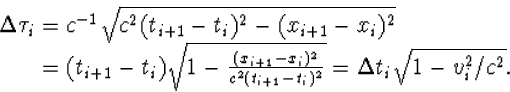 |
(6.11) |
Dit getal, een soort afstand tussen de twee punten, is onafhankelijk van
het gebruikte inertiaalsysteem. We bekijken vervolgens de som van deze getallen
voor alle intervallen tussen ta en tb. Dit geeft ons een langs
de wereldlijn gemeten benaderde ``afstand'' van ta naar tb, die ook nog
steeds Lorentz invariant is. Als we tenslotte het aantal tussenpunten laten
toenemen, gaat de som in de limiet van oneindig veel tussenpunten over in
een integraal:
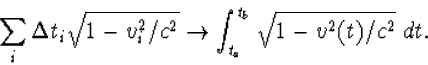 |
(6.12) |
Op deze manier hebben we een parametrisering van de wereldlijn van een
bewegend deeltje gekregen die in ieder inertiaalsysteem het zelfde is en op
dezelfde eenvoudige manier berekend wordt. We noemen deze parameter ![]() .Voor het 4-dimensionale geval krijgen we dan voor
.Voor het 4-dimensionale geval krijgen we dan voor ![]() als functie van t
de formule:
als functie van t
de formule:
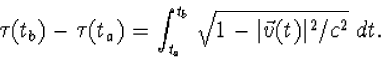 |
(6.13) |
Vanwege de extra factor c-1 in (6.11) heeft ![]() de dimensie van een
tijd. We zien direct uit formule (6.13) dat voor een deeltje in rust de
parameter met de gewone tijd samenvalt. Algemener geldt dat voor een eenparig
rechtlijnig bewegend deeltje
de dimensie van een
tijd. We zien direct uit formule (6.13) dat voor een deeltje in rust de
parameter met de gewone tijd samenvalt. Algemener geldt dat voor een eenparig
rechtlijnig bewegend deeltje ![]() de tijd is die gemeten wordt als men
overgaat naar het inertiaalsysteem waarin het deeltje in rust is, d.w.z.
het inertiaalsysteem dat met het deeltje meebeweegt. We noemen de parameter
de tijd is die gemeten wordt als men
overgaat naar het inertiaalsysteem waarin het deeltje in rust is, d.w.z.
het inertiaalsysteem dat met het deeltje meebeweegt. We noemen de parameter
![]() daarom de eigentijd.
daarom de eigentijd.
De eigentijd is niet alleen gedefiniëerd voor deeltjes die eenparig rechtlijnig bewegen; de integraal (6.13) kan natuurlijk ook berekend worden voor de gebogen wereldlijn van een deeltje met een snelheid die niet constant is. Ook in dit algemene geval interpreteren we de eigentijd als de tijd aangewezen door een met het deeltje meebewegende klok. Daarbij moet men wel een klok hebben die niet beinvloed wordt door de bij versnelling of vertraging optredende inertiaalkrachten. Een slingeruurwerk zou niet geschikt zijn. Het menselijk hart is natuurlijk ook niet geschikt, niet alleen vanwege de geringe nauwkeurigheid, maar vooral omdat het bij te grote inertiaal-krachten zal ophouden te functioneren. Wel geschikt zijn de atoomklokken die tegenwoordig algemeen gebruikt worden voor zeer nauwkeurige tijdsbepalingen.
Samengevat is de eigentijd de tijd van de met U meereizende klok. Het is deze
klok die bepaalt hoe oud U bent (hoe oud U zich voelt wordt door andere
parameters bepaald). Het is duidelijk dat de tijd die de met een waarnemer
meereizende klok aanwijst invariant is onder Lorentz transformatie - zo
geformuleerd is het een trivialiteit. Dit kan dus gebruikt worden als een meer
fysische definitie van het begrip eigentijd, en verklaart ook de naamgeving.
Het is vrij eenvoudig verg. (6.13) hieruit af te leiden. Deze formule is van
belang voor een waarnemer die bijvoorbeeld wil voorspellen hoe veel ouder U
bent geworden als U op ta hem verlaat, om op tb weer terug te keren. Als
we de tijd tussen twee tikken van de klok klein kiezen (en dt is willekeurig
klein), mogen we de snelheid tussen twee tikken constant veronderstellen,
zodat de tijd ![]() van de bewegende klok (Uw klok dus), verstreken tussen
twee tikken van de klok van de waarnemer, gegeven wordt door
van de bewegende klok (Uw klok dus), verstreken tussen
twee tikken van de klok van de waarnemer, gegeven wordt door
![]() . Al deze stukjes bij elkaar optellen
(integreren) geeft verg. (6.13).
. Al deze stukjes bij elkaar optellen
(integreren) geeft verg. (6.13).
Er zijn vele schijnbare tegenspraken die men met de relativiteitstheorie kan construeren. De nadruk ligt op het woord schijnbaar. Vaak blijkt dat men het begrip relativiteit te losjes pleegt te hanteren. U moet maar eens lezen wat Feynman daarover in zijn befaamde lectures zegt (Vol I, par. 16-1. Relativity and the philosophers). De meest bekende paradox is uiteraard die van de tweeling. Maar ik zal eerst wat andere voorbeelden noemen. Laat een hardloper een polsstok van 4 meter lengte evenwijdig aan de grond dragen en stel dat hij zo hard loopt dat voor een stilstaande waarnemen de polsstok een contractie met een factor twee ondergaat. De stok past daarbij in z'n geheel in een schuur van 2 meter lengte, waar de hardloper net aan voorbij raast. Vanuit zijn perspectief wordt echter diezelfde schuur verkort met een factor 2, en is nu slechts één meter, zodanig dat zijn stok maar liefst 4 schuren nodig heeft om opgeborgen te worden. Het probleem is natuurlijk dat op het moment dat we de stok als waarnemer in de schuur zien passen, de uiteinden van de stok voor de hardloper zelf niet gelijktijdig met de uiteinden van de schuur samenvallen. Men moet zich goed afvragen wat het betekent dat de stok in de schuur past.
Een ander voorbeeld is dat van twee ruimteschepen die door een stevig stuk kabel aan elkaar bevestigd zijn. Zij krijgen vanuit de aarde de opdracht om gelijktijdig hun motoren te ontsteken. We gaan ervan uit dat ze precies dezelfde versnelling ondergaan op ieder moment van de tijd. Toch is de bewering dat de kabel (of een van de ruimteschepen) zal breken.
Wat betreft de Lorentz contractie is het opmerkelijk dat het 50 jaar geduurd heeft eer iemand zich heeft afgevraagd hoe men nu een object waarneemt als het met grote snelheid voorbij komt. Omdat een object ook een eindige afmeting in de richting loodrecht op die van de beweging heeft, die geen contractie ondergaat, zoudt U op het eerste gezicht verwachten dat het vervormd wordt. Maar laten we eens wat zorgvuldiger kijken, aannemende dat we daarbij op zeer grote afstand van het object staan zodat alle lichtstralen uitgaande van dat object ons oog vanuit dezelfde richting bereiken. Maar dat betekent dat delen die verder van de waarnemer af zijn, het waargenomen licht iets eerder uitzonden, dan de delen die het dichtste bij de waarnemer liggen.
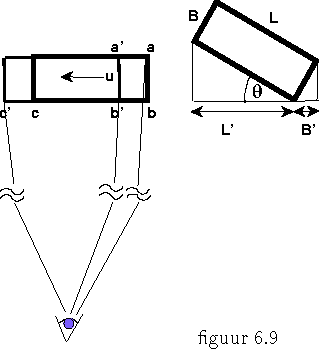
Dit is natuurlijk maar een heel klein tijdsverschil. Als het object een breedte
B heeft bedraagt dit tijdsverschil ![]() . Echter als de snelheid
dicht bij dit van het licht komt, dan heeft in die periode het object zelf
bijna dezelfde afstand B (in de richting van de snelheid) afgelegd. We zien
dus een verder afgelegen hoekpunt, a in de figuur, rechts van het
corresponderende (maar dichterbij gelegen hoekpunt) b. Op het moment van
waarnemen zien we (gelijktijdig) de ruimte-tijd gebeurtenissen corresponderende
met c', b' en a. Hierbij is dus de afstand c'-b' door de Lorentz
contractie verkort tot
. Echter als de snelheid
dicht bij dit van het licht komt, dan heeft in die periode het object zelf
bijna dezelfde afstand B (in de richting van de snelheid) afgelegd. We zien
dus een verder afgelegen hoekpunt, a in de figuur, rechts van het
corresponderende (maar dichterbij gelegen hoekpunt) b. Op het moment van
waarnemen zien we (gelijktijdig) de ruimte-tijd gebeurtenissen corresponderende
met c', b' en a. Hierbij is dus de afstand c'-b' door de Lorentz
contractie verkort tot ![]() en zien we de afstand b'-a als de
afstand
en zien we de afstand b'-a als de
afstand ![]() . Indien we nu de hoek
. Indien we nu de hoek ![]() invoeren, zodanig
dat
invoeren, zodanig
dat ![]() , dan komen L' en B' precies overeen met de
perspectivische verkorting van het zelfde object (in rust), waargenomen
onder een hoek
, dan komen L' en B' precies overeen met de
perspectivische verkorting van het zelfde object (in rust), waargenomen
onder een hoek ![]() met de oorspronkelijke bewegingsrichting. Dit
opmerkelijke feit hangt uiteraard samen met het feit dat
met de oorspronkelijke bewegingsrichting. Dit
opmerkelijke feit hangt uiteraard samen met het feit dat ![]() . Het werd voor het eerst beschreven door
J. Terrell in 1959.
. Het werd voor het eerst beschreven door
J. Terrell in 1959.
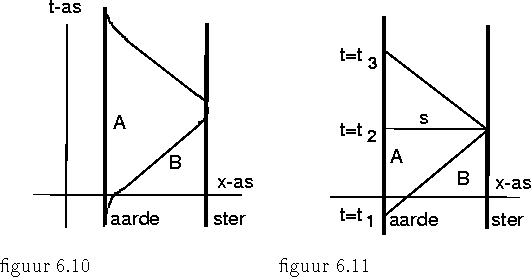
Van een tweeling onderneemt de éne broer, die we B zullen noemen, een ruimtereis. De andere broer (of zus), zeg A, blijft op aarde achter. We hebben dit enigszins schematisch getekend in figuur 6.10. B vliegt met een raket waarvan de snelheid die van het licht benadert naar een dichtbij gelegen ster en keert vervolgens weer naar de aarde terug. Hij maakt een veilige landing vlak bij het oorspronkelijke vertrekpunt en wordt daar welkom geheten door een oudere persoon, die hem bekend voorkomt. Na enig heen en weer gepraat en tot zijn grote verbazing blijkt het zijn broer A te zijn, die in zijn afwezigheid meer dan vijftien jaar ouder geworden is. B meent dat hij zelf slechts een paar maanden weg is geweest; dat leest hij af op zijn atoomklok, en zo voelt hij het zelf ook. Hij begrijpt niet hoe het mogelijk is dat A in de tussentijd zoveel ouder is geworden. A heeft jarenlang op de terugkeer van zijn broer gewacht en begrijpt er ook niets van.
We zullen nu laten zien dat het leeftijdsverschil, dat tussen de broers (of
zussen) is onstaan, logisch volgt uit hetgeen we in het voorafgaande over
tijdsmetingen hebben gezegd. Om de berekening zo eenvoudig mogelijk te
houden bezien we een enigszins geidealiseerde situatie. Deze is in figuur
6.11 getekend. B vertrekt op t=t1 van het punt x=0, bereikt onmiddelijk
een constante snelheid v en komt daarmee op tijdstip t=t2 aan bij een
ster die zich op een afstand s van de aarde bevindt. Er geldt natuurlijk
t2-t1=s/v. B onderneemt direct de terugreis, ook weer met de zelfde
constante snelheid v, en komt op aarde op zijn beginpunt terug op tijdstip
t3. Er geldt t3-t2=s/v. A ziet dus zijn broer terug keren op het
tijdstip t3, na een tijdsinterval ![]() . Dit alles is berekend
in het gegeven inertiaalsysteem, het systeem waarin de aarde en dus ook A
zich in rust bevinden. Om te weten welke tijden B gedurende zijn reis met
zijn eigen klok gemeten heeft moeten we naar de eigentijd langs zijn wereldlijn
kijken. Omdat de wereldlijn van B uit twee rechte lijnen bestaat kan de
integraal in formule (6.13) eenvoudig berekend worden: Als we de eigentijd
. Dit alles is berekend
in het gegeven inertiaalsysteem, het systeem waarin de aarde en dus ook A
zich in rust bevinden. Om te weten welke tijden B gedurende zijn reis met
zijn eigen klok gemeten heeft moeten we naar de eigentijd langs zijn wereldlijn
kijken. Omdat de wereldlijn van B uit twee rechte lijnen bestaat kan de
integraal in formule (6.13) eenvoudig berekend worden: Als we de eigentijd
![]() van B op het moment van zijn vertrek van de aarde nul stellen, dan is
van B op het moment van zijn vertrek van de aarde nul stellen, dan is
![]() op het moment van aankomst en vertrek op de ster, gelijk aan
op het moment van aankomst en vertrek op de ster, gelijk aan
![]() en vervolgens op het
ogenblik van terugkeer op aarde
en vervolgens op het
ogenblik van terugkeer op aarde ![]() .
.
We hebben dus gevonden dat er voor A tussen vertrek en terugkeer een
tijdsinterval ![]() is verstreken en volgens de klok van B
een korter tijdsinterval
is verstreken en volgens de klok van B
een korter tijdsinterval ![]() .Het is naïef is om te denken dat men een tegenspraak kan krijgen door de
redenering dat de situatie even goed vanuit tweeling B bekeken kan worden,
waardoor het B is die ouder geworden zou zijn. Zo'n redenering is niet juist.
De situatie is wat de rol van A en B betreft niet symmetrisch. De beweging
van B is op bepaalde momenten versneld of vertraagd, die van A niet. Dit
blijft zo in ieder ander inertiaalsysteem waarin men de situatie zou kunnen
bekijken.
.Het is naïef is om te denken dat men een tegenspraak kan krijgen door de
redenering dat de situatie even goed vanuit tweeling B bekeken kan worden,
waardoor het B is die ouder geworden zou zijn. Zo'n redenering is niet juist.
De situatie is wat de rol van A en B betreft niet symmetrisch. De beweging
van B is op bepaalde momenten versneld of vertraagd, die van A niet. Dit
blijft zo in ieder ander inertiaalsysteem waarin men de situatie zou kunnen
bekijken.
6.5 INTERMEZZO (gravitationele tijdsdilatatie)
De tegenspraak is dus alleen schijnbaar omdat slechts één van de tweelingen
een versnelling zal ondergaan, die nodig is om terug te keren naar zijn
beginpunt. Kennelijk is het zo dat een versnelling ook aanleiding geeft tot
tijdsdilatatie. Versnelling is equivalent met zwaartekracht, of zoals Einstein
het formuleerde, trage massa is gelijk aan gravitationele massa. Deels komt dit
door de keuze van Newton's gravitatieconstante, maar het feit dat deze
gelijkheid voor alle materie geldig is, maakt het tot een universele wet.
Hierdoor kunnen we (lokaal) geen onderscheid maken tussen een vrij vallende
lift en een intertiaalstelsel. De conclusie is dus kennelijk dat in een
gravitatieveld klokken langzamer lopen. Dit kan met een heel eenvoudig
voorbeeld geillustreerd worden. Om in een ruimtestation gravitatie te
simuleren kan men het laten ronddraaien, zodanig dat in de woon- en
werkruimtes de centrifugale versnelling precies gelijk is aan de
gravitatieversnelling op aarde (dus ongeveer 10 m/s2). Vanuit een
stilstaande waarnemer bezien, zeg iemand in het centrum van het ronddraaiende
ruimtestation, waar geen centrifugale versnelling optreedt (dus waar de
``zwaartekracht'' nul is) bewegen de klokken in de woon- en werkruimten,
bevestigd aan de roterende wand van het ruimtestation, met een snelheid die
gelijk is aan ![]() , waarin
, waarin ![]() de hoeksnelheid is. Die klokken
ondergaan dus een tijdsdilatatie met een factor
de hoeksnelheid is. Die klokken
ondergaan dus een tijdsdilatatie met een factor ![]() .
Dit kan ook geschreven worden als
.
Dit kan ook geschreven worden als ![]() , waarin
, waarin
![]() precies de centrifugale potentiaal is, ofwel de
arbeid die men per massa-eenheid verricht als men tegen de centrifugale
potentiaal in van een woonruimte op de wand naar het midden van het
ruimtestation reist (de centrifugale versnelling bedraagt
precies de centrifugale potentiaal is, ofwel de
arbeid die men per massa-eenheid verricht als men tegen de centrifugale
potentiaal in van een woonruimte op de wand naar het midden van het
ruimtestation reist (de centrifugale versnelling bedraagt ![]() , zodat
, zodat ![]() ).
Volgens Einstein is dit equivalent met een gravitatieveld. Het punt dat geen
kracht ondervindt bevindt zich natuurlijk niet langer in het (graviterende)
centrum, maar in oneindig. Immers Newton's gravitatiewet zegt dat de kracht
afvalt omgekeerd evenredig met het kwadraat van de afstand. Om de
tijdsdilatatie in een gravitatieveld te berekenen kunnen we dus de centrifugale
potentiaal vervangen door de gravitationele potentiaal (per eenheid van massa),
Vgrav=GM/r. We concluderen dus dat de klokken in een gravitatieveld
langzamer lopen en dat de tijdsdilatatie gegeven wordt door
).
Volgens Einstein is dit equivalent met een gravitatieveld. Het punt dat geen
kracht ondervindt bevindt zich natuurlijk niet langer in het (graviterende)
centrum, maar in oneindig. Immers Newton's gravitatiewet zegt dat de kracht
afvalt omgekeerd evenredig met het kwadraat van de afstand. Om de
tijdsdilatatie in een gravitatieveld te berekenen kunnen we dus de centrifugale
potentiaal vervangen door de gravitationele potentiaal (per eenheid van massa),
Vgrav=GM/r. We concluderen dus dat de klokken in een gravitatieveld
langzamer lopen en dat de tijdsdilatatie gegeven wordt door
![]() . Dit is precies het resultaat dat men kan afleiden uit
Einstein's algemene relativiteitstheorie. Merk op dat bij r=2GM/c2 de klok
stil komt te staan. Deze straal, tegenwoordig bekend als de
Schwarzschild straal, is ook de straal waar de ontsnappingsnelheid precies
gelijk aan de lichtsnelheid is. Laplace had zich al gerealiseerd dat een
ster mogelijk zo compact kon worden dat licht niet van haar oppervlak kan
ontsnappen. Hij noemde dit zwarte sterren. Nu noemen we het zwarte gaten.
Doordat de tijd bij de Schwarzschild straal stil staat (het oppervlak dat
daarmee correspondeert heet de horizon) kan niets uit het inwendige ontsnappen.
Het lijkt alsof er een gat in de ruimte-tijd zit.
. Dit is precies het resultaat dat men kan afleiden uit
Einstein's algemene relativiteitstheorie. Merk op dat bij r=2GM/c2 de klok
stil komt te staan. Deze straal, tegenwoordig bekend als de
Schwarzschild straal, is ook de straal waar de ontsnappingsnelheid precies
gelijk aan de lichtsnelheid is. Laplace had zich al gerealiseerd dat een
ster mogelijk zo compact kon worden dat licht niet van haar oppervlak kan
ontsnappen. Hij noemde dit zwarte sterren. Nu noemen we het zwarte gaten.
Doordat de tijd bij de Schwarzschild straal stil staat (het oppervlak dat
daarmee correspondeert heet de horizon) kan niets uit het inwendige ontsnappen.
Het lijkt alsof er een gat in de ruimte-tijd zit.
We kunnen eigentijd ook definiëren als er krachten op een object werken, zolang de eigentijd maar gedefinieerd wordt als de tijd gemeten in een lokaal Lorentz stelsel. Dat betekent strikt gesproken dat onze standaard tijd een heel kleine correctie behoeft om de eigentijd uit af te leiden.
Nu een paar getallen: Als doel van de reis kiezen we Sirius, één van de
sterren, die zich betrekkelijk dicht bij de aarde bevinden. De afstand van
Sirius tot de aarde is 8,8 lichtjaren. (Een lichtjaar is de afstand die het
licht in 1 jaar aflegt, dus ![]() ). Voor de snelheid van het ruimteschip nemen we
). Voor de snelheid van het ruimteschip nemen we ![]() .
Omdat v zeer weinig van de lichtsnelheid c verschilt is
.
Omdat v zeer weinig van de lichtsnelheid c verschilt is ![]() nagenoeg gelijk aan
nagenoeg gelijk aan ![]() jaar. De factor v/c is
jaar. De factor v/c is ![]() , dus v2/c2 is nagenoeg
, dus v2/c2 is nagenoeg ![]() , dus
, dus ![]() en
en ![]() . Daarmee
wordt
. Daarmee
wordt ![]() gelijk aan ruim 4 maanden.
gelijk aan ruim 4 maanden.
Een ruimtereis, over deze afstand en met een dergelijke snelheid, ligt voorlopig nog ver buiten onze mogelijkheden. Bij minder ambitieuze proefnemingen, die men met de huidige techniek zou kunnen realiseren - denk bijvoorbeeld aan reizen met onbemande ruimtevaartuigen door het zonnestelsel - is het te verwachten effect nog veel te klein. Toch beschikken we over een rechtstreekse experimentele bevestiging van het door de tweeling paradox, of klok paradox, voorspelde tijdsverschil. Al in 1971 hebben de amerikanen Hafele en Keating dit huzarenstukje voor elkaar gekregen door met een Cesiumklok als medepassagier een vliegreis (gewoon met een lijnvliegtuig!) om de aarde te maken, zowel in westelijke als in oostelijke riching. Door de twee richtingen te nemen kan men effecten t.g.v. het gravitatieveld en de draaiing van de aarde nauwkeurig aftrekken van het resultaat en heeft men op een netto vliegtijd van bijna 100 uur (dat kan tegenwoordig toch heel wat sneller) een tijdsverschil gemeten van ongeveer 150 nanoseconden, in goede overeenstemming met de speciale relativiteitstheorie. Bij deeltjesversnellers is het dagelijkse kost deze tijdsdilatatie op een juiste manier mee te nemen, anders zouden de versnellers niet eens werken!