Het probleem hier is dat we aannemen dat de voor- en achterkant van de doos gelijktijdig gaan bewegen, of stoppen. Maar gelijktijdigheid hangt van de bewegingstoestand af. Het zou ook betekenen dat er informatie van de ene naar de andere kant wordt gestuurd met een oneindige snelheid, hetgeen in strijd is met het feit dat niets sneller kan dan het licht. In de praktijk merken we hier niets van, omdat het gaat om zeer kleine effecten en verplaatsingen. Toch werpt dit een smet op dit mooie gedachtenexperiment. We bespreken daarom nu een betere variant om tot E=mc2 te komen.
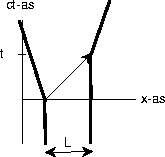
We ontkoppelen de twee wanden en noemen het nu blokken, die we ieder dezelfde massa M geven (terwijl ze bewegen). Nu is er alleen een terugstoot bij het linker blok, met v=-E/(Mc). Het rechter blok blijft stil staan, zodat het licht een afstand L moet overbruggen (zie de figuur), dus t=L/c. Bij de absorptie krijgt het rechter blok een beweging naar rechts, en omdat de massa dezelfde is als die van het linker blok, is diens snelheid in grootte gelijk, v=E/(Mc).

Na absorptie bewegen het linker en rechter blok in tegengestelde richtingen met precies dezelfde snelheid. Omdat ze ook precies dezelfde massa hebben beweegt, zoals het hoort, het zwaartepunt niet. Tussen het moment van emissie en absorptie van het licht beweegt alleen het linkerblok over een afstand x=-vt=-EL/(Mc2), zie de figuur. De eis dat het zwaartepunt op zijn plaats blijft is nu Mx+mL=0 (het rechter blok draagt niet bij, omdat het zich niet verplaatst). Dat hieruit wederom E=mc2 volgt is nu triviaal.