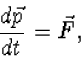
Eén van de grondgedachten van de relativiteitstheorie is dat ruimte en tijd nauw met elkaar verbonden begrippen zijn. Ze vormen samen één 4-dimensionale ruimte, waarvan de punten bestaan uit gebeurtenissen. Deze zijn in verschillende inertiaalsystemen voorzien van verschillende ruimte-tijd coördinaten, die door Lorentz transformaties zijn verbonden. In overeenstemming hiermee kan men in de relativiteitstheorie voor allerlei begrippen en grootheden een 4-dimensionale vorm kiezen. Dit heeft grote voordelen. We krijgen compacte en transparante formuleringen en de relativistische eigenschappen worden duidelijk zichtbaar. We hebben dat bijvoorbeeld gezien bij de begrippen energie en impuls die we in één Lorentz 4-vector konden samenvatten.
We gaan uit van de bewegingsvergelijking (8.1), die we schrijven als
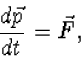 |
(8.24) |
met de ![]() de impuls. Newton heeft zelf al zijn wet geformuleerde
als kracht is de verandering van impuls. Duidelijk is dat deze wet
geldig is bij lage snelheden. We weten dat
de impuls. Newton heeft zelf al zijn wet geformuleerde
als kracht is de verandering van impuls. Duidelijk is dat deze wet
geldig is bij lage snelheden. We weten dat ![]() deel is van een 4-vector
deel is van een 4-vector
![]() , en evenals bij de bepaling van de snelheids 4-vector is
duidelijk dat
, en evenals bij de bepaling van de snelheids 4-vector is
duidelijk dat ![]() weer een Lorentz 4-vector is. We kunnen
aldus een Lorentz 4-vector
weer een Lorentz 4-vector is. We kunnen
aldus een Lorentz 4-vector ![]() invoeren, die de rol van
relativistische kracht moet spelen
invoeren, die de rol van
relativistische kracht moet spelen
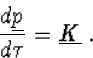 |
(8.25) |
Aangezien
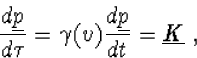 |
(8.26) |
zodat kennelijk
| (8.27) |
Net als de impuls 4-vector ![]() , heeft de relativistische kracht
slechts drie onafhankelijke componenten. Immers, dp0/dt=c-1dE/dt en
dE/dt is de verrichtte arbeid per tijdseenheid. Arbeid is kracht maal
afgelegde afstand, zodat arbeid per tijdseenheid gegeven wordt door kracht
maal snelheid
, heeft de relativistische kracht
slechts drie onafhankelijke componenten. Immers, dp0/dt=c-1dE/dt en
dE/dt is de verrichtte arbeid per tijdseenheid. Arbeid is kracht maal
afgelegde afstand, zodat arbeid per tijdseenheid gegeven wordt door kracht
maal snelheid
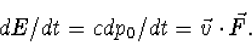 |
(8.28) |
Inderdaad kunnen we dit afleiden uit verg. (8.24):
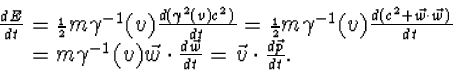 |
(8.29) |
Hierbij gebruikten we op slinkse wijze dat ![]() ,
, ![]() en dat
en dat
![]() . Dit laatste bewijst men
eenvoudig door het inwendig product in componenten uit te schrijven.
Aangezien
. Dit laatste bewijst men
eenvoudig door het inwendig product in componenten uit te schrijven.
Aangezien ![]() , hebben we nu het bewijs van verg.
(8.28) rond. In termen van
, hebben we nu het bewijs van verg.
(8.28) rond. In termen van ![]() hebben we dus
hebben we dus
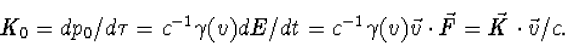 |
(8.30) |
Een willekeurige relativisitische kracht wordt kennelijk verkregen
door, uitgaande van het (lokale) ruststelsel, te transformeren met de
Lorentz transformatie van verg. (4.41), gebruikmakende van een snelheid
![]() (in de richting van de kracht). In het
ruststelsel wordt de (gewone) Newtonse kracht,
(in de richting van de kracht). In het
ruststelsel wordt de (gewone) Newtonse kracht, ![]() ,
gebruikt (de index o is om te benadrukken dat
,
gebruikt (de index o is om te benadrukken dat ![]() de kracht in het ruststelsel is gedefinieerd). De 4-vector
de kracht in het ruststelsel is gedefinieerd). De 4-vector ![]() wordt dan gegeven door
(0,Fo1,Fo2,Fo3).
Dus verg. (8.25) kan als een relativistische bewegingsvergelijking gezien
worden. In deze formulering is het duidelijk dat de wet van Newton niet fout
is; het is alleen van belang duidelijk te maken in welk stelsel deze kan
worden toegepast - in het lokale Lorentz stelsel (ruststelsel) dus, dat
uiteraard tijdens de beweging verandert.
wordt dan gegeven door
(0,Fo1,Fo2,Fo3).
Dus verg. (8.25) kan als een relativistische bewegingsvergelijking gezien
worden. In deze formulering is het duidelijk dat de wet van Newton niet fout
is; het is alleen van belang duidelijk te maken in welk stelsel deze kan
worden toegepast - in het lokale Lorentz stelsel (ruststelsel) dus, dat
uiteraard tijdens de beweging verandert.
Een van de postulaten van de relativiteitstheorie, bevat in de definitie van
een intertiaalstelsel is, dat een deeltje waar geen krachten op werken, zich
eenparig rechtlijnig voortbeweegt, dus met constante snelheid. Is nu ![]() een willekeurige andere kracht, zodanig dat in het ruststelsel de krachten
precies in balans zijn, dan is er ook een balans in alle andere stelsels.
een willekeurige andere kracht, zodanig dat in het ruststelsel de krachten
precies in balans zijn, dan is er ook een balans in alle andere stelsels.
Beschouw als voorbeeld een ruimteschip, dat een constante versnelling ondergaat.
Hier is het meest voor de hand liggend uitgangspunt het ruststelsel, immers het
is in dat stelsel dat de kracht wordt uitgeoefend (bepaald door de stuwkracht
t.o.v. het ruimteschip). We nemen voor het gemak de versnelling in de
x-richting, met een waarde a=Fo/m. Er geldt dus ![]() , met
, met ![]() en K0=vK1/c, zodat
en K0=vK1/c, zodat ![]() .
Aangezien
.
Aangezien ![]() en
en ![]() , volgt
, volgt
![]() =0. Dit heeft (met x(t=0)=v(t=0)=0 als randvoorwaarde)
=0. Dit heeft (met x(t=0)=v(t=0)=0 als randvoorwaarde)
![]() als oplossing. Hieruit is nu v=dx/dt als functie van
x te vinden,
als oplossing. Hieruit is nu v=dx/dt als functie van
x te vinden,
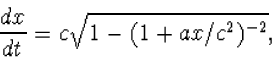 |
(8.31) |
waarmee we x(t) bepalen (probeer dit na te gaan):
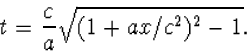 |
(8.32) |
Voor t klein, geeft dit het niet-relativistische resultaat, ![]() .
Uit verg. (8.31) zien we eenvoudig dat de snelheid, v=dx/dt, begrensd is door
de lichtsnelheid, die voor
.
Uit verg. (8.31) zien we eenvoudig dat de snelheid, v=dx/dt, begrensd is door
de lichtsnelheid, die voor ![]() van onderen wordt benaderd.
We kunnen constante versnelling (
van onderen wordt benaderd.
We kunnen constante versnelling (![]() ,
, ![]() )
ook bekijken vanuit een inertiaalstelsel, zoals voor de hand ligt bij
een geladen deeltje in een electrisch veld, waarover later meer. We kiezen
wederom de kracht in de x-richting en definiëren
a=F/m. Nu geldt
dw1 /dt=a, zodat
)
ook bekijken vanuit een inertiaalstelsel, zoals voor de hand ligt bij
een geladen deeltje in een electrisch veld, waarover later meer. We kiezen
wederom de kracht in de x-richting en definiëren
a=F/m. Nu geldt
dw1 /dt=a, zodat ![]() , We bepalen hieruit weer de snelheid
v=dx/dt,
, We bepalen hieruit weer de snelheid
v=dx/dt,
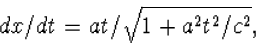 |
(8.33) |
zodat
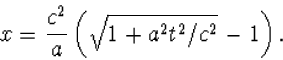 |
(8.34) |
Wederom gaat men eenvoudig na dat voor t klein, het niet-relativistische
resultaat (de parabool ![]() ) volgt en dat de snelheid begrensd is
door de lichtsnelheid. In beide gevallen geldt
) volgt en dat de snelheid begrensd is
door de lichtsnelheid. In beide gevallen geldt
| [1+ax(t)/c2]2-[at/c]2=1. | (8.35) |