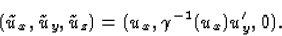- 3.
- a.
- We gebruiken
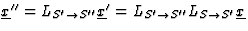 en de formules (4.37) en
(4.39) uit de syllabus:
en de formules (4.37) en
(4.39) uit de syllabus:
| 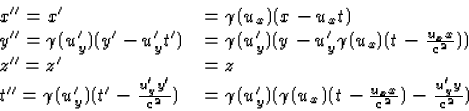 |
(14) |
- b.
- Op analoge wijze bepalen we de inverse transformatie
| 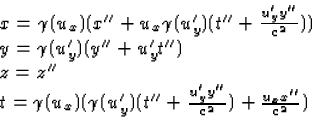 |
(15) |
Voor een vast punt (x'',y'',z'',t'')=(a,b,c,t'') volgen we nu dezelfde weg
als bij opg. (1.b.ii) en lossen t'' op als functie van t m.b.v. vgl. (15).
Dit geeft 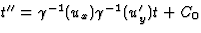 . Voor de coordinaten
in S van het vaste punt in S'' vinden we dan
. Voor de coordinaten
in S van het vaste punt in S'' vinden we dan
| 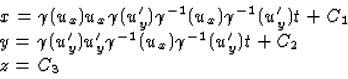 |
(16) |
met 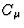 ,
, 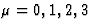 functies van a,b,c,ux,u'y, dus constanten
m.b.t. de ruimte-tijd coordinaten. Alleen de voorfactoren van ruimte-tijd
coordinaten behoeven een precieze bepaling als we de snelheid willen weten!
Deze lezen we nu direct af:
functies van a,b,c,ux,u'y, dus constanten
m.b.t. de ruimte-tijd coordinaten. Alleen de voorfactoren van ruimte-tijd
coordinaten behoeven een precieze bepaling als we de snelheid willen weten!
Deze lezen we nu direct af:
| 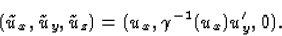 |
(17) |
Vergelijk dit met opgave (1.b.ii) met vx=vy=vz=0. Zoals bij opgave 1 is
het ook hier eenvoudiger gebruik te maken van de kettingregel om de snelheden
uit te rekenen.
- c.
- We vergelijken vgl. (14) met de uitdrukking voor de algemene standaard Lorentz transformatie
formule (4.41) uit de syllabus. In formule (4.41) is de voorfactor van y in
de uitdrukking voor x' gelijk aan de voorfactor van x in de uitdrukking
van y', L12=L21, zie de notatie in hfst. 7. In vgl. (14), met
x''=Lx, is zo'n symmetrie er niet, ergo vgl. (14) is géén zuivere
Lorentz transformatie. Met een draaiing in het xy vlak is dit op te vangen. I.h.a. geldt dat
twee achtereenvolgende zuivere Lorentz transformaties in verschillende richtingen een
combinatie vormt van een zuivere Lorentz transformatie en een rotatie. U begrijpt nu waarom.
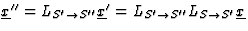 en de formules (4.37) en
(4.39) uit de syllabus:
en de formules (4.37) en
(4.39) uit de syllabus:
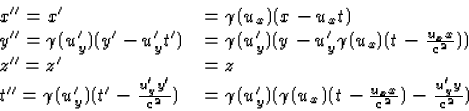
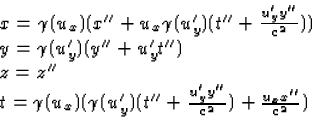
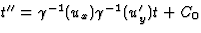 . Voor de coordinaten
in S van het vaste punt in S'' vinden we dan
. Voor de coordinaten
in S van het vaste punt in S'' vinden we dan
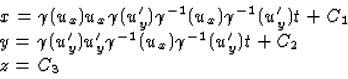
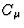 ,
, 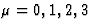 functies van a,b,c,ux,u'y, dus constanten
m.b.t. de ruimte-tijd coordinaten. Alleen de voorfactoren van ruimte-tijd
coordinaten behoeven een precieze bepaling als we de snelheid willen weten!
Deze lezen we nu direct af:
functies van a,b,c,ux,u'y, dus constanten
m.b.t. de ruimte-tijd coordinaten. Alleen de voorfactoren van ruimte-tijd
coordinaten behoeven een precieze bepaling als we de snelheid willen weten!
Deze lezen we nu direct af: