- 5.
- a.
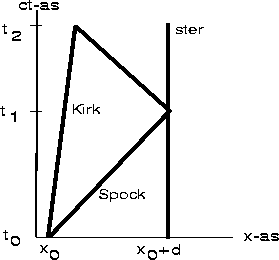
- We bepalen eerst de posities xK(t) en xS(t) van Kirk en Spock. Kirk
beweegt met snelheid v in de positieve x-richting:
Voor Spock geldt
| 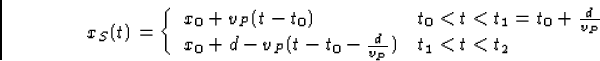 |
(20) |
U hebt de keus om vP t.o.v. het ruimteschip of t.o.v.
S te nemen. We kiezen hier vP t.o.v. S
voor de heenweg, en -vP t.o.v.
S voor de terugweg. Verklaring van vgl. (20): in het
interval t0<t<t1 reist Spock naar de ster. Hij komt na een tijd d/vP
aan, dus op 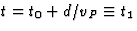 . Hij is dan ter plaatse x=x0+d. Daarna,
t1<t<t2, reist hij terug. We berekenen nu t2 door xS(t2)=xK(t2)
te stellen. We vinden dan
. Hij is dan ter plaatse x=x0+d. Daarna,
t1<t<t2, reist hij terug. We berekenen nu t2 door xS(t2)=xK(t2)
te stellen. We vinden dan
| 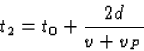 |
(21) |
De plaats van ontmoeting x2 verkrijgen we nu als xK(t2) of xS(t2),
x2=x0+2dv/(v+vP).
Bezien vanuit Kirk is deze berekening wat ingewiddelder. Voor hem heeft
Spock op de heenreis een snelheid v'P=(vP-v)/(1-vvP/c2) en op de
terugreis v"P=(vP+v)/(1+vvP/c2). Voor Kirk is de afstand tot de
ster verkort tot 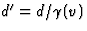 . Spock ontmoet de ster als v'P(t'-t'0)=
x'S(t')=x'ster(t')=d'-v(t'-t'0), dus voor
. Spock ontmoet de ster als v'P(t'-t'0)=
x'S(t')=x'ster(t')=d'-v(t'-t'0), dus voor 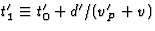 .
Spock komt terug op het tijdstip t'2=t'1+x'S(t'1)/v"P, zodat de totale
reistijd van Spock, zoals gemeten door Kirk, gegeven wordt door
.
Spock komt terug op het tijdstip t'2=t'1+x'S(t'1)/v"P, zodat de totale
reistijd van Spock, zoals gemeten door Kirk, gegeven wordt door 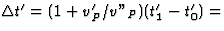 d'(1+v'P/v"P)/(v'P+v)=
d'(1+v'P/v"P)/(v'P+v)= 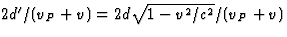 .
.
- b.
- We maken gebruik van formules (6.11) en (6.13) uit de syllabus. We vinden dan
| 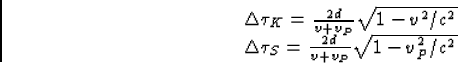 |
(22) |
De verhouding is 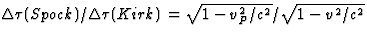 . Kirk is bij terugkomst ouder, omdat vP>v. Bezien vanuit Kirk
is uiteraard
. Kirk is bij terugkomst ouder, omdat vP>v. Bezien vanuit Kirk
is uiteraard 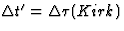 , hetgeen dus overeenstemt met wat we
vanuit S gezien vonden. Verder geldt vanuit Kirk bezien dat
, hetgeen dus overeenstemt met wat we
vanuit S gezien vonden. Verder geldt vanuit Kirk bezien dat
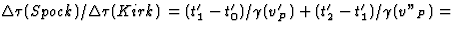
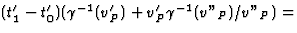
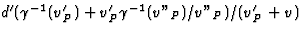 . Dit vergt wat meer
rekenwerk, maar ook hier kan men laten zien dat we het eerder bepaalde
resultaat terugvinden.
. Dit vergt wat meer
rekenwerk, maar ook hier kan men laten zien dat we het eerder bepaalde
resultaat terugvinden.
Het is duidelijk dat de berekening vanuit Kirk's standpunt veel moeilijker
is. Echter dit ligt anders als we de snelheid (vP) van Spock niet t.o.v.
S, maar t.o.v. Kirk definiëren - in de praktijk ligt dit ook voor
de hand. Anderzijds, bij het terugkeren van Spock ligt het meer voor de
hand om de snelheid (-vP) van Spock te kiezen t.o.v. de ster (dus
t.o.v. S). Probeer nu zelf het verloop van de tijd uit te rekenen voor deze
situatie (dus met vP de snelheid van vertrek t.o.v. Kirk en bij terugkeer
-vP de snelheid t.o.v. de ster).
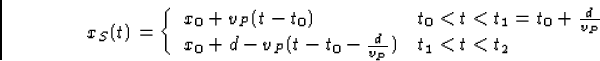
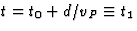 . Hij is dan ter plaatse x=x0+d. Daarna,
t1<t<t2, reist hij terug. We berekenen nu t2 door xS(t2)=xK(t2)
te stellen. We vinden dan
. Hij is dan ter plaatse x=x0+d. Daarna,
t1<t<t2, reist hij terug. We berekenen nu t2 door xS(t2)=xK(t2)
te stellen. We vinden dan
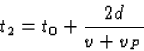
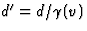 . Spock ontmoet de ster als v'P(t'-t'0)=
x'S(t')=x'ster(t')=d'-v(t'-t'0), dus voor
. Spock ontmoet de ster als v'P(t'-t'0)=
x'S(t')=x'ster(t')=d'-v(t'-t'0), dus voor 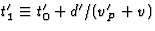 .
Spock komt terug op het tijdstip t'2=t'1+x'S(t'1)/v"P, zodat de totale
reistijd van Spock, zoals gemeten door Kirk, gegeven wordt door
.
Spock komt terug op het tijdstip t'2=t'1+x'S(t'1)/v"P, zodat de totale
reistijd van Spock, zoals gemeten door Kirk, gegeven wordt door 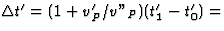 d'(1+v'P/v"P)/(v'P+v)=
d'(1+v'P/v"P)/(v'P+v)= 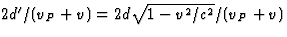 .
.

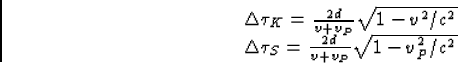
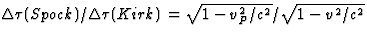 . Kirk is bij terugkomst ouder, omdat vP>v. Bezien vanuit Kirk
is uiteraard
. Kirk is bij terugkomst ouder, omdat vP>v. Bezien vanuit Kirk
is uiteraard 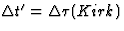 , hetgeen dus overeenstemt met wat we
vanuit S gezien vonden. Verder geldt vanuit Kirk bezien dat
, hetgeen dus overeenstemt met wat we
vanuit S gezien vonden. Verder geldt vanuit Kirk bezien dat
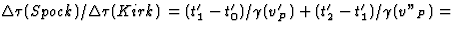
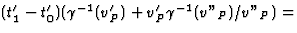
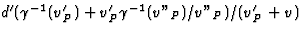 . Dit vergt wat meer
rekenwerk, maar ook hier kan men laten zien dat we het eerder bepaalde
resultaat terugvinden.
. Dit vergt wat meer
rekenwerk, maar ook hier kan men laten zien dat we het eerder bepaalde
resultaat terugvinden.