- ... oppervlakte-afleiding1
- Voorwaar geen oppervlakkige afleiding! Voor meer moois over deze stelling
verwijs ik U naar de lezing van Prof. Tijdeman.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... opgevallen.2
- Ik verwijs hier natuurlijk naar objectieve tijdswaarneming. Voor het
gevoel gaat de tijd juist langzaam als men stilstaat.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bespreken.3
- Het woord paradox wordt hier in zijn juiste betekenis gebruikt,
namelijk een schijnbare tegenstelling.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... afgevuurd.4
- De spiegel dreigt daarbij te sneuvelen, weliswaar na de voltooiing van het
experiment!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lezen.5
- Zie
http://www.lorentz.leidenuniv.nl/research/vanbaal/DECEASED/SRT/vwo/vwo.html voor een opgave
die U stap voor stap naar het antwoord leidt. Het staat in zijn geheel
uitgewerkt in mijn propedeuse collegedictaat speciale relativiteitstheorie
http://www.lorentz.leidenuniv.nl/research/vanbaal/DECEASED/SRT/syllabus/title.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... massa.6
- Vervang een van de biljartballen door een die precies even groot is, maar
een ander gewicht heeft, en U zult zien hoe zelfs een ervaren biljarter er een
potje van maakt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... afstand7
- Er zijn hier wat kleine vereenvoudigingen gemaakt, zoals het feit dat de
achterkant van de doos tegelijk met de voorkant in beweging komt. Maar al die
vereenvoudigingen vallen tegen elkaar weg, en wat we concluderen is
precies goed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... energie.8
- Zoals U op pijnlijke wijze zult ondervinden bij een botsing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dus9
- U kunt nu zelf nagaan dat inderdaad
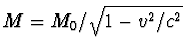
,
door bijvoorbeeld gebruik te maken van
Mc2=m'c2+m0c2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
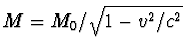 ,
,