De basisformule van de Newtonse mechanica, de relatie ![]() , is niet
invariant onder Lorentz transformaties. Dat betekent dat de Newtonse mechanica
niet past in de Einsteinse relativiteitstheorie. Dit hebben we in hoofdstuk 4
expliciet laten zien door de transformatie van de versnelling te bestuderen.
Zie ook de korte samenvattende conclusie aan het einde van hoofdstuk 5.
, is niet
invariant onder Lorentz transformaties. Dat betekent dat de Newtonse mechanica
niet past in de Einsteinse relativiteitstheorie. Dit hebben we in hoofdstuk 4
expliciet laten zien door de transformatie van de versnelling te bestuderen.
Zie ook de korte samenvattende conclusie aan het einde van hoofdstuk 5.
We gaan in dit hoofdstuk de basisbegrippen formuleren van een nieuwe mechanica, die aan de eisen van de speciale relativiteitstheorie voldoet, en die we daarom Einsteinse mechanica kunnen noemen. Zoals we al eerder opgemerkt hebben blijft de Newtonse mechanica bruikbaar als een zeer goede benadering voor een groot gebied van fysische verschijnselen, in feite voor de meeste verschijnselen van mechanische aard die we om ons heen kunnen waarnemen. Pas bij situaties waarbij extreem hoge snelheden optreden, zoals bijvoorbeeld in de deeltjesversnellers, die men voor experimenten in de elementaire deeltjesfysica gebruikt, moet de Newtonse mechanica vervangen worden door de nieuwe Einsteinse mechanica. (Om begrijpelijke redenen spreekt men vaak van niet-relativistische en relativistische mechanica. Strikt genomen is de aanduiding Newtonse en Einsteinse mechanica beter. Beide zijn namelijk relativistisch in de zin dat ze aan een bepaalde versie van het relativiteitsprincipe voldoen.)
We zullen ons in onze discussie beperken tot het geval van puntdeeltjes. In het tweede deel bespreken we ook de invloed van een electromagnetisch veld op geladen deeltjes. (We hebben gezien dat gelijktijdigheid van twee gebeurtenissen op verschillende plaatsen geen Lorentz invariant begrip is. Het idee van twee deeltjes die elkaar op afstand beïnvloeden door een instantane krachtswerking, hoort daarom niet thuis in het kader van de relativiteitstheorie. Wisselwerking door middel van gravitatiekrachten kan pas volledig bevredigend worden beschreven als men gebruik maakt van de algemene relativiteitstheorie, die door Einstein in 1912 is geintroduceerd, en die kan worden opgevat als een uitbreiding van zijn speciale relativiteitstheorie.)
De beweging van een puntdeeltje wordt beschreven door 3 functies van t,
x1(t), x2(t) en x3(t). Op ieder moment hoort daarbij een snelheids
3-vector ![]() met componenten vj(t)=dxj(t)/dt.
De basisformule van de Newtonse mechanica,
met componenten vj(t)=dxj(t)/dt.
De basisformule van de Newtonse mechanica,
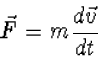 |
(8.1) |
zegt dat de verandering van deze snelheid evenredig is aan de kracht die op het deeltje wordt uitgeoefend. Voor het vinden van relativistische modificaties van niet-relativistische formules gaan we over naar een 4-dimensionale beschrijving. We proberen in het bijzonder om 3-vectoren te vervangen door Lorentz 4-vectoren. Van formules die met behulp van 4-vectoren geschreven zijn kunnen we direct zien hoe ze transformeren onder Lorentz transformaties.
We kijken naar de snelheid: We hebben de drie componenten vj(t)=dxj(t)/dt.
Het ligt voor de hand om te proberen hiervan een 4-vector te maken door deze
drie componenten aan te vullen met een component v0(t)=dx0(t)/dt. Omdat
x0(t)=ct betekent dat v0(t)=c. Dus de vraag is of
| (8.2) |
een Lorentz 4-vector vormt. Dat dit niet het geval is zien we door op te merken
dat ![]() . Zoals gewoonlijk schrijven we
. Zoals gewoonlijk schrijven we
![]() voor de lengte van de 3-snelheidsvector. Gebruiken we dat
voor de lengte van de 3-snelheidsvector. Gebruiken we dat
![]() , dan zien we dat de 4-vector
, dan zien we dat de 4-vector
| (8.3) |
wel een invariante ``lengte'' heeft,
| (8.4) |
Bedenk ook dat ![]() een Lorentz 4-vector is, maar dat t niet
invariant is onder Lorentz transformaties, zodat
een Lorentz 4-vector is, maar dat t niet
invariant is onder Lorentz transformaties, zodat ![]() nooit
als een Lorentz 4-vector kan transformeren. Als nu
nooit
als een Lorentz 4-vector kan transformeren. Als nu ![]() de een willekeurige
andere parameter is, waarin we de bewegingen van het deeltje beschrijven,
de een willekeurige
andere parameter is, waarin we de bewegingen van het deeltje beschrijven,
![]() , dan geeft
differentiatie naar
, dan geeft
differentiatie naar ![]() wel een Lorentz 4-vector, immers men heeft voor
een Lorentz transformatie L (gebruik dat
wel een Lorentz 4-vector, immers men heeft voor
een Lorentz transformatie L (gebruik dat ![]() constant is)
constant is)
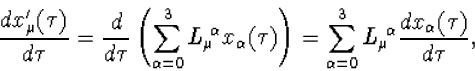 |
(8.5) |
en dit komt overeen met formule (7.18), die het transformatiegedrag van
Lorentz 4-vectoren beschrijft. We nemen nu als parameter de in hoofdstuk 6
ingevoerde eigentijd. Met behulp van formule (6.13) vinden we
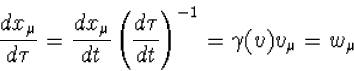 |
(8.6) |
Dit betekent dat we te maken hebben met grootheden, die voor snelheden v
die klein zijn ten opzichte van de lichtsnelheid c niet merkbaar verschillen
van de componenten van ![]() . De volgende definitie ligt daarom voor de hand:
. De volgende definitie ligt daarom voor de hand:
| De 4-snelheidsvector van een bewegend puntdeelje is een 4-vector
w met de componenten |
|---|
De 4-snelheid bevat natuurlijk maar 3 onafhankelijke componenten. Dat zien we
bijvoorbeeld aan het feit dat de ``lengte'' van ![]() gelijk aan c
is.
gelijk aan c
is.
De definitie van de snelheids 4-vector is nog een zuiver kinematische
aangelegenheid, nl. de beschrijving van de beweging van een deeltje. We gaan
nu een stapje nemen in de richting van een relativistische dynamica,
door naast de 4-snelheid de impuls als 4-vector nader te bestuderen. Ook in de
Newtonse mechanica speelt de impuls een belangrijke rol.
De impulsvector ![]() van een deeltje met snelheid
van een deeltje met snelheid ![]() en massa
m is gelijk aan
en massa
m is gelijk aan ![]() . We definiëren in analogie hiermee een
4-vector:
. We definiëren in analogie hiermee een
4-vector:
De relativistische 4-impulsvector van een deeltje met massa m
is de 4-vector
|
|---|
Als de snelheid v van het deeltje klein is ten opzichte van de lichtsnelheid
c geldt natuurlijk dat de ![]() componenten van deze relativistische
4-impuls
componenten van deze relativistische
4-impuls ![]() experimenteel niet te onderscheiden zijn van de
componenten van de niet-relativistische impuls
experimenteel niet te onderscheiden zijn van de
componenten van de niet-relativistische impuls ![]() . We kunnen dit
expliciet maken door de factor
. We kunnen dit
expliciet maken door de factor ![]() naar ordes v2/c2 te ontwikkelen
volgens
naar ordes v2/c2 te ontwikkelen
volgens
| (8.8) |
Voor de ![]() componenten van p geeft dit
componenten van p geeft dit
| (8.9) |
De nulde orde term is de niet-relativistische impuls, de hogere orde termen zijn correcties daarop.
De impuls is een belangrijk begrip in de Newtonse mechanica. Dat komt vooral
omdat het onder geschikte omstandigheden een behouden grootheid is. Van een
veeldeeltjes-systeem, dat geen uitwendige krachten ondervindt, zijn de drie
componenten van de totale impuls constant in de tijd. In botsingsprocessen is
de totale impuls vóór de botsing gelijk aan de totale impuls ná de
botsing: Als we de deeltjes nummeren met de index k, de massa's aangeven
met m(k), de grootheden vóór de botsing aangeven als ![]() ,
,![]() , en ná de botsing als
, en ná de botsing als ![]() ,
, ![]() , betekent
dit
, betekent
dit
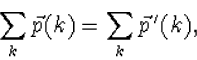 |
(8.10) |
of uitgeschreven
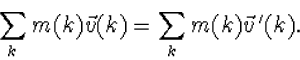 |
(8.11) |
De wet van het behoud van impuls kan afgeleid worden uit de bewegingsvergelijkingen van Newton; het is een belangrijke dynamische eigenschap van niet-relativistische systemen.
We nemen aan dat er iets soortgelijks geldt voor het relativistische geval:
| We veronderstellen dat in de relativistische mechanica de j = 1,2,3
componenten van de 4-impuls |
|---|
Voor een botsingsproces betekent dat
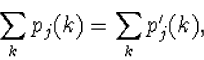 |
(8.12) |
of anders geschreven
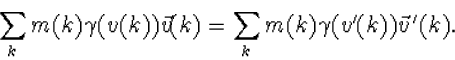 |
(8.13) |
Het is experimenteel gebleken, dat formule (8.11) niet meer geldig is bij botsingsprocessen waarbij de deelnemende deeltjes zeer hoge snelheden hebben. In plaats daarvan vindt men dat bij zulke processen voldaan wordt aan de zojuist geformuleerde relativistische behoudswet. Formule (8.13) beschrijft dus een belangrijke dynamische eigenschap van relativistische systemen.
De 4-impulsvector ![]() heeft vier componenten. We hebben er tot
dusver maar drie besproken. Wat is de fysische betekenis van de vierde
component p0? Daartoe ontwikkelen we cp0 naar v2/c2 met behulp
van (8.8). Dat geeft
heeft vier componenten. We hebben er tot
dusver maar drie besproken. Wat is de fysische betekenis van de vierde
component p0? Daartoe ontwikkelen we cp0 naar v2/c2 met behulp
van (8.8). Dat geeft
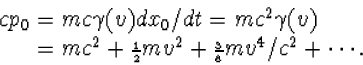 |
(8.14) |
Afgezien van een constante term mc2, die alleen afhangt van de massa, dus
van het soort deeltje, vinden we de niet-relativistische (kinetische)
energie van het deeltje ![]() , en tenslotte termen van hogere orde
in v2/c2, die we als relativistische correctietermen kunnen opvatten.
Dit maakt aannemelijk dat we cp0 de relativistische (kinetische)
energie noemen:
, en tenslotte termen van hogere orde
in v2/c2, die we als relativistische correctietermen kunnen opvatten.
Dit maakt aannemelijk dat we cp0 de relativistische (kinetische)
energie noemen:
| De energie van een vrij bewegend puntdeeltje is volgens de
relativiteitstheorie gelijk aan cp0, met p0 de vierde component van
de relativistische 4-impulsvector |
|---|
Bij een botsingproces van deeltjes met hoge snelheden is het deze grootheid
die behouden is, zoals uit vele experimenten is gebleken. Er geldt dus
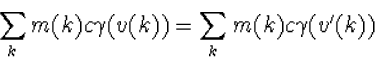 |
(8.15) |
en niet
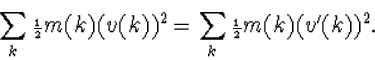 |
(8.16) |
Opmerking: In de relativiteitstheorie zijn impuls en energie nauw met elkaar verbonden: er is één 4-vectorgrootheid, de energie-impuls 4-vector. Deze is uit de vier afzonderlijke grootheden opgebouwd. Het onderscheid tussen wat energie is en wat impuls hangt van de bewegingstoestand van de waarnemer af, net als bij het onderscheid tussen tijd en ruimte in de Minkowski ruimte.
Aan het eind van het vorige hoofdstuk hebben we gezien dat voor een foton
![]() en
en ![]() . Hieruit leiden we eenvoudig af dat
. Hieruit leiden we eenvoudig af dat
| E=p c. | (8.17) |
Als er één natuurkundige wet is die iedere leek kent, dan is het wel de beroemde wet van equivalentie tussen massa en energie
| E=mc2. | (8.18) |
Omgekeerd correspondeert massa met energie, en is dus de conclusie dat zelfs
een deeltje in rust een energie heeft. Omdat c zo groot is, is die energie
gigantisch en ligt E=mc2 aan de basis van het verkrijgen van energie uit
kernreacties, zowel bij fusie als bij splijting. Anderzijds, als we een
deeltje een snelheid v geven neemt zijn energie toe. Naast de rustenergie
mc2 komt er de kinetische energie bij, ![]() . Deze energie
vertegenwoordigt op zijn beurt een massa
. Deze energie
vertegenwoordigt op zijn beurt een massa ![]() . We hebben
al eerder gezien dat de Newtonse wetten alleen geldig zijn bij kleine snelheden,
zodat we verwachten dat de formule voor m(v) alleen geldig is voor snelheden
klein t.o.v. de lichtsnelheid. Tot in laagste orde komt bovenstaande resultaat
overeen met
. We hebben
al eerder gezien dat de Newtonse wetten alleen geldig zijn bij kleine snelheden,
zodat we verwachten dat de formule voor m(v) alleen geldig is voor snelheden
klein t.o.v. de lichtsnelheid. Tot in laagste orde komt bovenstaande resultaat
overeen met ![]() . Deze formule is juist daarom acceptabel omdat
het verklaart waarom een deeltje niet sneller dan de lichtsnelheid kan gaan.
De trage massa m(v) wordt steeds groter met toenemende snelheid en gaat bij
nadering van de lichtsnelheid naar oneindig, zodanig dat een versnelling
alleen nog maar ten goede komt aan de toenemende massa m(v) maar niet meer
aan een toenemende snelheid.
. Deze formule is juist daarom acceptabel omdat
het verklaart waarom een deeltje niet sneller dan de lichtsnelheid kan gaan.
De trage massa m(v) wordt steeds groter met toenemende snelheid en gaat bij
nadering van de lichtsnelheid naar oneindig, zodanig dat een versnelling
alleen nog maar ten goede komt aan de toenemende massa m(v) maar niet meer
aan een toenemende snelheid.
Een eenvoudig bewijs van deze formule voor m(v) kan gegeven worden door gebruik te maken van het feit dat de impuls en de energie behouden moet blijven bij een botsing. Men heeft wel eens geprobeerd deze behoudswetten omver te werpen. Vooral bij het beta (of radioactieve) verval zat men lange tijd met het probleem dat impuls- en energiebehoud met elkaar in tegenspraak waren, tot dat Pauli op het idee kwam dat dit wel eens zou kunnen komen doordat men blind was voor een extra deeltje dat bij het vervalsproces betrokken was, namelijk het neutrino. Dit heeft zulke zwakke interacties met andere materie (het heeft geen electrische lading en mogelijk geen rustmassa, in welk geval het zich altijd met de lichtsnelheid voortbeweegt), dat we het niet zien. Er is een belangrijke reden om behoud van energie en impuls als onschendbare wetten te beschouwen. Ze zijn een consequentie van het feit dat ruimte en tijd homogeen zijn. We nemen aan dat de natuurwetten invariant zijn onder translatie in ruimte en tijd. (Evenzo volgt uit de isotropie van de ruimte, oftewel de invariantie onder een draaiing, dat het impulsmoment behouden moet zijn.) We bekijken nu de botsing van twee identieke deeltjes met massa m en exact tegengestelde snelheden w. De deeltjes zijn voorzien van zeer sterke kleefpasta, zodanig dat ze niet meer los van elkaar kunnen komen en dus na de botsing als één deeltje stil blijven liggen. Immers de totale impuls voor de botsing was nul. We nemen aan dat er geen wrijving is opgetreden en dat bij het aan elkaar kleven geen warmte wordt geproduceerd. We gaan nu over van het zwaartepuntstelsel naar het ruststelsel van één van de twee deeltjes (zie de figuur).
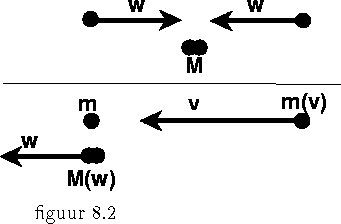
Klassiek zou het andere deeltje nu een snelheid 2w hebben, maar uit het relativistisch optellen van de snelheden volgt dat in dit nieuwe stelsel het andere deeltje beweegt met een snelheid
| v=2w/(1+w2/c2). | (8.19) |
We noemen de nader te bepalen massa m(v). Na de botsing hebben de twee
samenklittende deeltjes een snelheid w en een massa M(w) (immers het
zwaartepuntstelsel heeft een snelheid w t.o.v. het nieuwe stelsel). Uit
behoud van energie en impuls volgt
| (8.20) |
Uit deze twee vergelijkingen kunnen we M(w) elimineren, waartoe we de vergelijking voor energiebehoud met w/c2 vermenigvuldigen, (m+m(v))w= M(w)w. Dit substituren in de vergelijking voor impulsbehoud geeft dus (m(v)+m)w=m(v)v.
Samen met v=2w/(1+w2/c2) volgt dus (ga na!)
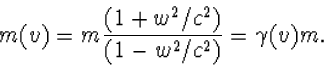 |
(8.21) |
Hoewel we dit resultaat hebben verkregen zonder te bepalen wat M(w) in werkelijkheid is, is het toch interessant deze te berekenen.
We hebben nu gezien dat E=m(v)c2 en ![]() en dat we deze
grootheden kunnen combineren in een 4-vector, genoemd de 4-impuls
en dat we deze
grootheden kunnen combineren in een 4-vector, genoemd de 4-impuls
![]() , die zich onder Lorentz transformaties op
de juiste manier gedraagt. Dit in analogie met de situatie voor het foton.
De ``lengte'' van deze tijdachtige 4-vector is precies de rustmassa
maal de lichtsnelheid, een resultaat dat onafhankelijk is van het stelsel
(dus van de snelheid v). Het stelsel waarin de ruimtelijke componenten
verdwijnen is precies het lokale inertiaalstelsel, dat ook gedefinieerd
is in aanwezigheid van gravitatiekrachten.
, die zich onder Lorentz transformaties op
de juiste manier gedraagt. Dit in analogie met de situatie voor het foton.
De ``lengte'' van deze tijdachtige 4-vector is precies de rustmassa
maal de lichtsnelheid, een resultaat dat onafhankelijk is van het stelsel
(dus van de snelheid v). Het stelsel waarin de ruimtelijke componenten
verdwijnen is precies het lokale inertiaalstelsel, dat ook gedefinieerd
is in aanwezigheid van gravitatiekrachten.
Opmerking: We kunnen de relativistische energie E uitdrukken in
de j=1,2,3 componenten van de 4-impuls. We gebruiken hiervoor het resultaat
uit opgave 22. Met ![]() lossen we E op uit
lossen we E op uit ![]() . Dit geeft de relativistische
energie-impuls relatie
. Dit geeft de relativistische
energie-impuls relatie
| (8.22) |
Een belangrijke eigenschap van het boven ingevoerde energiebegrip is de aanwezigheid van de constante term mc2 in de uitdrukking van de energie van een vrij deeltje: zoals we eerder zagen betekent het dat er ook een energie wordt toegekend aan een deeltje dat in rust is. Omdat het hier om een constante gaat die alleen van het soort deeltje afhangt, zou men kunnen denken dat men deze rustenergie ook wel weg zou kunnen laten. Dit is niet het geval. Integendeel, de extra term heeft te maken met een zeer belangrijk fysische aspect van de relativiteitstheorie dat nog niet ter sprake gekomen is. Bij het spreken over botsingsprocessen hebben we tot nog toe stilzwijgend aangenomen dat het om elastische processen ging, d.w.z. om processen waarbij men voor en na de botsing de zelfde deeltjes heeft, alleen met andere snelheden en zich in andere richtingen bewegend. In die situatie kan men in formule (8.15), de behoudswet voor de relativistische energie in een botsingsproces, de rustenergietermen van de linkerkant en van de rechterkant aftrekken, zonder dat de geldigheid van de formule wordt aangetast.
In de kernfysica en in de elementaire deeltjesfysica kent men ook
niet-elastische processen waarbij ingaande en uitkomende deeltjes
verschillend zijn; er heeft creatie en annihilatie van deeltjes plaats.
Denk bijvoorbeeld aan een geval waarbij er twee deeltjes a en b ingaan, en
er tengevolge van wisselweking tijdens de botsing drie andere deeltjes A,
B en C uitkomen. Dit is typisch een situatie waarbij de
relativiteitstheorie gebruikt moet worden. Er is behoud van energie in de
relativistische zin, d.w.z. er geldt
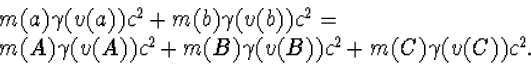 |
(8.23) |
Als we in deze formule de termen voor de rustenergie van linker en rechterlid aftrekken, geldt het gelijkteken in het algemeen niet meer. Dat betekent dat in dit geval de rustenergie essentiëel is voor de geldigheid van het principe van energiebehoud.
We kunnen dit ook nog een beetje anders zien: In een proces zoals beschreven in (8.23) is het mogelijk dat de totale massa verandert; m(a)+m(b) hoeft niet gelijk te zijn aan m(A)+m(B)+m(C). Wat het zelfde blijft is de totale energie; de massa maakt daar deel van uit. Dat er inderdaad fysische processen mogelijk zijn, waarbij daadwerkelijk massa in energie en energie in massa kan worden omgezet, is pas vele jaren na het formuleren van de speciale relativiteitstheorie, bij het tot ontwikkeling komen van de kernfysica en later de elementaire deeltjesfysica, duidelijk geworden.
We vatten dit belangrijke aspect van de relativiteitstheorie kort samen:
| Volgens de speciale relativiteitstheorie is massa een vorm van energie. Massa en energie kunnen in principe in elkaar overgevoerd worden volgens de relatie E=mc2. De kernfysica en de elementaire deeltjesfysica hebben dat ook daadwerkelijk mogelijk gemaakt. |
|---|
Opmerking: Men gebruikt soms twee massabegrippen naast elkaar, nl.
een rustmassa die men aangeeft als m0, en die overeenkomt met wat wij de
massa m hebben genoemd, en een massa m gedefiniëerd als ![]() die wij m(v) hebben genoemd. In dat geval kan men zeggen dat de massa van
een deeltje afhangt van zijn snelheid.
die wij m(v) hebben genoemd. In dat geval kan men zeggen dat de massa van
een deeltje afhangt van zijn snelheid.
We hebben in dit hoofdstuk enkele grondbegrippen van de relativistische
mechanica ingevoerd aan de hand van behoudswetten voor energie en impuls.
Voor een deeltje, dat zich in een electromagnetisch veld beweegt, is het
mogelijk om verder te gaan. Men kan in dat geval een 4-dimensionale
generalisatie geven van de formule ![]() , de basisformule
van de Newtonse mechanica. Hierbij voert men een 4-dimensionale versie van
het begrip kracht in. We zullen er in het volgende hoofdstuk enkele
opmerkingen over maken.
We geven een overzicht van de belangrijkste resultaten:
, de basisformule
van de Newtonse mechanica. Hierbij voert men een 4-dimensionale versie van
het begrip kracht in. We zullen er in het volgende hoofdstuk enkele
opmerkingen over maken.
We geven een overzicht van de belangrijkste resultaten:
| De relativistische energie en impuls van een deeltje met massa m worden
beschreven door één Lorentz 4-vector De componenten van Voor snelheden v die veel kleiner zijn dan de lichtsnelheid c kunnen we naar v2/c2 ontwikkelen: De energie van het deeltje kan worden uitgedrukt in |
|---|